Calculating Support Reactions for a Beam with Inclined Resting Position

[dbag123]

Homework Statement

Calculate the support reactions

Relevant Equations

ΣFx =0
ΣFy=0
ΣMa=0
ΣMb=0

Hello

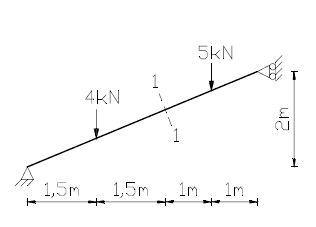I have a problem with calculating the support reactions for a beam. Lefts side of beam has a pin connection so it takes both Fx,Fy. Right side of the beam has a horizontal roller and it takes only Fy in the direction of the wall. Therefore at the pin support Fy=9kN, but how do i figure out the reactions for X-direction?

I thought about the X-component as a tangent to the 2 point loads so 5kN/tan(21.8);4kN/tan(21.8)5kN/tan(21.8);4kN/tan(21.8) and they give me 12,5 and 10kN respectively. I don't know if they are correct and if they are how do they distribute to each support?

I can also think of another way of doing this and that is by making the beam horizontal and turning the roller support 68.2 degrees, then calculating the reactions ΣMa=0: -4kN*1.5m-5kN*4m+By*5m=0 5,2kN By and 13kN for Bx and ΣMb=0: 4kN*3.5m+5kN*1m-Ay*5m=0 it comes out to 3,8kN for Ay 9,5kN to Ax. These components are parallel to the beam itself. Is either of these methods correct?
Thanks

 

[Chestermiller]

Your second idea of taking moments makes sense, but why do you need to reorient the beam to the horizontal position? What does the moment balance about the lower support look like?

 

[dbag123]

reorienting the beam was just a test to see if i got the same results as the solution suggests and its quite close and as far as the moment about pin support A goes and By then is the reaction perpendicular to the beam at the roller support:
ΣMa=0: -4kN*1.5m-5kN*4m+By*5m=0

 

[Chestermiller]

reorienting the beam was just a test to see if i got the same results as the solution suggests and its quite close and as far as the moment about pin support A goes and By then is the reaction perpendicular to the beam at the roller support:
ΣMa=0: -4kN*1.5m-5kN*4m+By*5m=0

The moment arm for B is 2 meters.

 

[dbag123]

The moment arm for B is 2 meters.

and that is how the roller get its 13kN. Thank you very much.