How Do You Calculate the Effective Spring Constant k_eff for Springs in Series?

Click For Summary
SUMMARY

The effective spring constant \( k_{eff} \) for springs in series can be calculated using the formula \( \frac{1}{k_{eff}} = \frac{1}{k_1} + \frac{1}{k_2} \). This relationship establishes that the total extension of the spring system is the sum of the extensions of each individual spring, represented as \( F = k_{eff}(x_1 + x_2) \). The discussion emphasizes the importance of understanding the behavior of springs in series to derive the correct expression for \( k_{eff} \).

PREREQUISITES
  • Understanding of Hooke's Law and spring mechanics
  • Familiarity with the concept of series and parallel spring systems
  • Basic algebra for manipulating equations
  • Knowledge of force and displacement relationships in mechanical systems
NEXT STEPS
  • Research the derivation of effective spring constants for parallel spring systems
  • Explore advanced applications of spring systems in mechanical engineering
  • Learn about energy storage in spring systems and its implications
  • Investigate real-world examples of spring systems in automotive suspension design
USEFUL FOR

Mechanical engineers, physics students, and anyone studying mechanical systems involving springs and their properties.

ksmith159
Messages
2
Reaction score
0
See attached file:
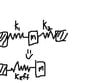
I would like to show theoretically that the first double spring system is equivalent to the second system with only one spring keff. Then I want to derive an expression for keff in terms of k1 and k2.

I think this system is in series and therefore keff =1/k1 +1/k2
but that is probably not even close to the right track...
 

Attachments

  • keff.jpg
    keff.jpg
    11.1 KB · Views: 603
Physics news on Phys.org
Well for the new spring system

F=k_{eff}(x_1+x_2)

knowing that F is the same for both springs, can you make an attempt now?

(sorry if I sound harsh,am a bit handicapped at the moment and typing is tedious)
 

Similar threads

How Do You Calculate the Speed of a Mass in an Oscillating System?
  • · Replies 4 ·
Replies
4
Views
2K
Finding effective spring constants
  • · Replies 2 ·
Replies
2
Views
4K
Classical mechanics:effective spring const
  • · Replies 9 ·
Replies
9
Views
3K
I am glad I could help.Effective spring constant for two springs and a pulley
  • · Replies 13 ·
Replies
13
Views
12K
How Do You Calculate the Natural Angular Frequency of a Dual-Spring System?
  • · Replies 5 ·
Replies
5
Views
3K
Energy stored in a double spring system
  • · Replies 17 ·
Replies
17
Views
1K
Spring Problem Involving Variables and Constants Only
  • · Replies 3 ·
Replies
3
Views
2K
Frequency of an oscillating mass with springs in series
  • · Replies 1 ·
Replies
1
Views
14K
Multiple choice Q: Mangetic fields and Spring Constant
  • · Replies 8 ·
Replies
8
Views
2K
Equivalent Spring Constant in Series and Parallel Configurations
  • · Replies 15 ·
Replies
15
Views
24K