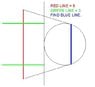
How Do You Calculate the Length of a Chord and Tangential Line in a Circle?
Click For Summary
SUMMARY
The discussion focuses on calculating the lengths of a chord and a tangential line in a circle using geometric principles. The key data provided includes a circle radius of 2, a red line of length 6, and a green line of length 3. The solution involves applying the tangent-chord theorem and the Pythagorean theorem, leading to the conclusion that the length of the chord is 3.82 units. The use of sine functions and isomorphic triangles is also highlighted as part of the solution process.
PREREQUISITES- Understanding of basic geometry concepts, including circles and tangents.
- Familiarity with the Pythagorean theorem.
- Knowledge of the tangent-chord theorem.
- Ability to work with trigonometric functions, specifically sine.
- Study the tangent-chord theorem in detail to understand its applications.
- Learn how to derive the lengths of segments in circles using the Pythagorean theorem.
- Explore isomorphic triangles and their properties in geometric proofs.
- Practice solving problems involving trigonometric functions in geometric contexts.
Students studying geometry, educators teaching circle theorems, and anyone interested in solving geometric problems involving chords and tangents.
Similar threads
- · Replies 9 ·
- · Replies 7 ·
- · Replies 11 ·
- · Replies 3 ·
- · Replies 13 ·
Undergrad
Average chord length of a circle
- · Replies 7 ·
- · Replies 13 ·