mathmari
Gold Member
MHB
- 4,984
- 7
Hey! 
We are given the following letters with the respective frequencies:
\begin{equation*}\begin{matrix}a/2 & b/4 & c/7 & d/6 & e/4 & f/5 & g/8 & h/10 & i/3 & j/11\end{matrix}\end{equation*}
For that I have applied the Huffman code and I got the following tree:
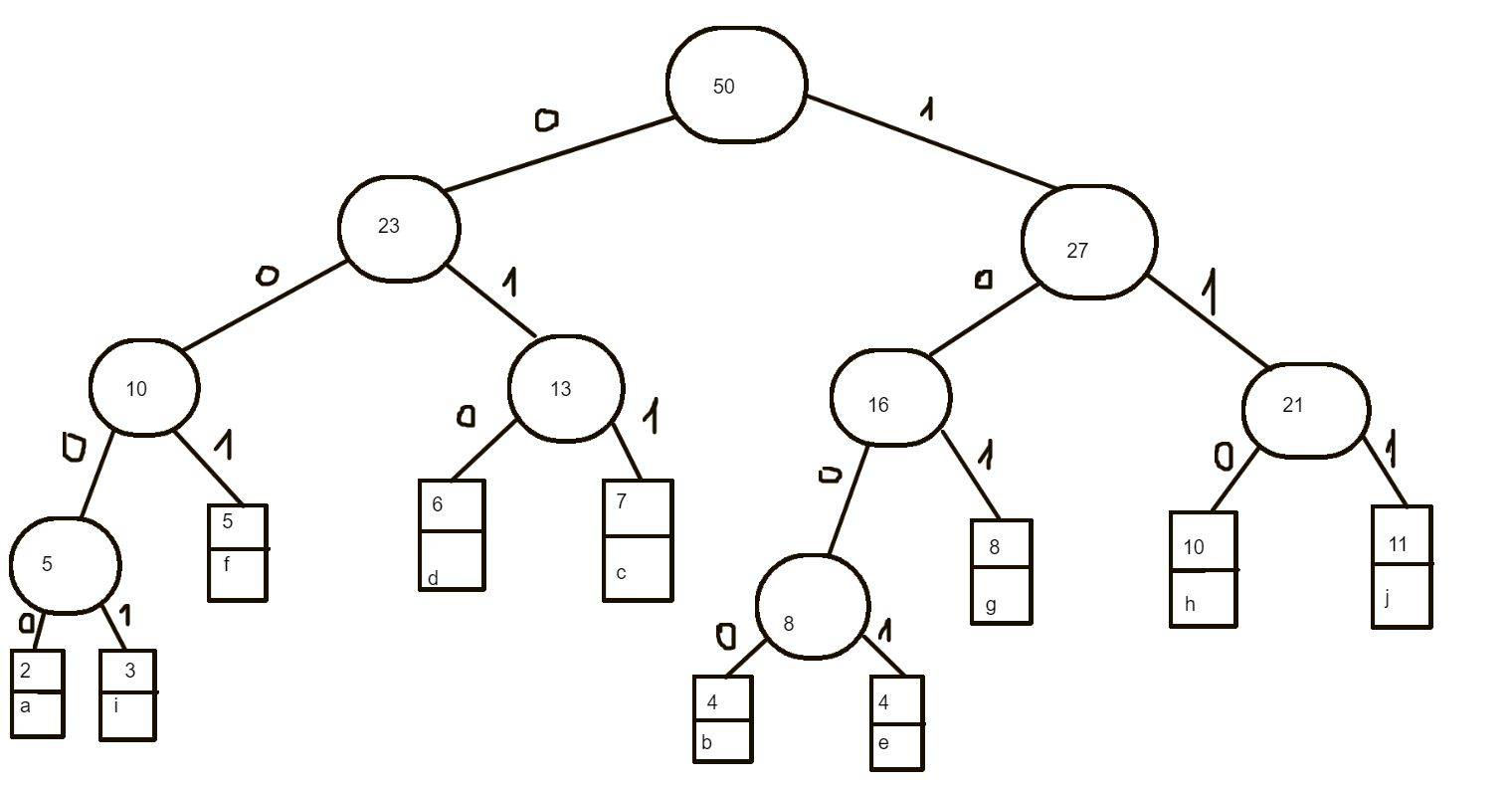 Now it is asked for the total weight of the code. How do we calculate that? :unsure:
Now it is asked for the total weight of the code. How do we calculate that? :unsure:
We are given the following letters with the respective frequencies:
\begin{equation*}\begin{matrix}a/2 & b/4 & c/7 & d/6 & e/4 & f/5 & g/8 & h/10 & i/3 & j/11\end{matrix}\end{equation*}
For that I have applied the Huffman code and I got the following tree: