How Do You Calculate Torques for a Ladder in Static Equilibrium?

[penroseandpaper]

Homework Statement

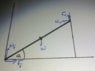
A ladder of length 'L' is leant against a wall, making an angle of 'a' with the horizontal. There are five forces acting on it (normal from floor, friction from floor, weight in centre of ladder, normal off wall and friction on wall), and the coefficient of static friction is 0.6 at both points.

The ladder is in mechanical equilibrium and axis of rotation is at the centre of mass, thus write down the components of the forces that act as torques, state which way the resultant torque acts (into or out of the screen) and calculate the smallest angle for which the ladder won't slide.

Relevant Equations

No net force
No net torque

Torque = r × F

Hi everyone,

I'm studying an introductory physics course at college, but our teacher is off sick. On top of that, a planned strike means we won't be getting a new science tutor until the start of next month - instead, we've been told to read the textbook and answer the questions. I've got up to torques and have now hit a brick wall. I was wondering if you'd be kind enough to provide me a few pointers on a practice question to which I don't have a solution to or an answer?

Firstly, a few overall questions:

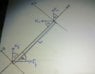
•Am I right in thinking there are 4 torques at play - a component of all forces, minus weight?

•When I'm resolving them, do I make the ladder equivalent to the X axis? Does this mean all the torques are represented by L × Force × sin 'a' (I've attached an image of my sketch to this effect)?

•Does the resultant torque make the ladder come away from the wall rather than sliding down it? If it falls backwards, the torque would act out of the screen - I believe.

•How do we determine which torques are positive and which are negative - on my sketch, it would only be the friction on the floor that is negative?

Second, is my sketch of resolving the forces correct? I wasn't sure if I'm right to assume those angles are also 'a', although the wall ones has to be due to the right angle between the forces and straight line equalling 180°. Or whether that's how you go about it when the lever arm is at an angle.

I haven't got to the angle bit yet, so shall refrain from questions for now.

Thank you very much for your assistance,
Penn

 

[haruspex]

there are 4 torques at play

Yes.

do I make the ladder equivalent to the X axis?

Your choice, but I wouid not do that here since all four forces you are asked to discriminate are vertical or horizontal.

Does the resultant torque make the ladder come away from the wall rather than sliding down it?

It is static, so the net force and net torque are zero.

How do we determine which torques are positive and which are negative

I don't know which sense you are taking as positive.
(I note that you have the wall on the right; I would have drawn it on the y axis.)
Can you not just look at each force in turn, imagine the ladder on an axle at its centre and figure out which way the force wouid tend to rotate the ladder?

wasn't sure if I'm right to assume those angles are also 'a',

No. You have misled yourself by drawing it with an angle close to 45 degrees. Try a more general position.

 

[Cutter Ketch]

The ladder is static, so you can say any point is the axis of rotation (because, after all, it isn’t rotating about any point). If you choose a different point you can work with fewer torques.

As to the sign of the torques, the sign is determined by which way the torque is trying to spin the ladder about the selected axis: clockwise vs counterclockwise. You can choose either direction as positive if you are consistent.