gracy
- 2,486
- 83
I have to draw a contact angle.
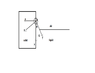
Actually I've to detect the edge of the droplet first. It looks like a semicircle. Then I've to draw a tangent which gives me the contact angle.But I am not getting how to draw a tangent.I know a tangent is a line or plane which touches a given curve or solid at a single point.I want to know what will be that single point in my case(i.e in drawing contact angle)?The image below will depict my problem more clearly

Why not theta in red contact angle rather than black one?
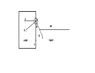
Actually I've to detect the edge of the droplet first. It looks like a semicircle. Then I've to draw a tangent which gives me the contact angle.But I am not getting how to draw a tangent.I know a tangent is a line or plane which touches a given curve or solid at a single point.I want to know what will be that single point in my case(i.e in drawing contact angle)?The image below will depict my problem more clearly
Why not theta in red contact angle rather than black one?