Discussion Overview
The discussion revolves around finding the centroid of a region bounded by specific curves and calculating the hydrostatic force on a trapezoidal gate in an irrigation canal. Participants explore mathematical approaches and formulas related to these topics, including integration and the identification of functions.
Discussion Character
- Technical explanation
- Mathematical reasoning
- Homework-related
- Debate/contested
Main Points Raised
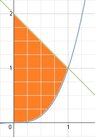
- One participant presents a problem involving finding the centroid of the region bounded by the curves $y=x^{3}$, $x+y=2$, and $x=0$.
- Another participant describes the trapezoidal gate's dimensions and asks for the hydrostatic force on one side of the gate.
- Several participants discuss the linear relationship of the width of the plate as a function of depth, proposing the equation $w(x)=5-x$ based on given points.
- There is uncertainty expressed by participants regarding the material covered in class and the clarity of the textbook explanations.
- Participants derive the formula for the hydrostatic force and set up the integral $\int_{0}^{2} 62.5x(5-x)\,dx$ for calculation.
- Discussion includes identifying limits and functions for the centroid calculation, with some participants struggling to understand the definitions and methods used in their textbooks.
- One participant corrects a previous formula provided, noting that it applies only under certain conditions.
Areas of Agreement / Disagreement
Participants express varying levels of understanding and comfort with the material, with some agreeing on the formulas to use while others remain confused about the application and definitions. No consensus is reached on the best approach to the problems presented.
Contextual Notes
Participants mention different methods and formulas for calculating the centroid, indicating potential confusion stemming from varying textbook approaches. There is also an acknowledgment of the need for clarity in understanding the functions involved in the calculations.