- #1
harpazo
- 208
- 16
I decided to review a few calculus 1 topics of interest. I like related rates but setting up the proper equation has been a big problem for me.
Question:
A light is on top of a building that is 15 ft. high. A man, 6 ft. tall, is walking away from the building at the rate of 2 ft/sec. At what rate is the shadow of the man changing when he is 4 ft. away from the building?
My Work:
This is a related rates problem given by the hint "At what rate is the shadow of the man changing..."
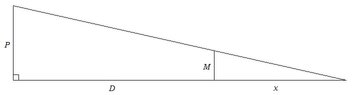
I think a similar triangle set up is needed here.
(Height of building)/(height of man) = y/(y - x), where y is the distance from the building to the man and (y - x) is the distance of the man's shadow.
NOTE: SHOULD THE DENOMINATOR BE (y - x) or (y + x)?
What's the difference?
The proportion then becomes
15/6 = y/(y - x)
Solving for y, I get y = (5x/3).
I now must differentiate both sides with
respect to time t, then substitute in what I know for the values of the variables. Since I want the speed of the shadow, I want to find out what dy/dt equals.
d/dt [y] = d/dt [(5x/3)
dy/dt = (dx/dt)(5/3)
I am given that dx/dt = 2 feet per second.
dy/dt = 2(5/3)
dy/dt = 10/3 ft/sec
Can I also write the answer as
dy/dt = 3.33 feet per second?
Is any of this correct?
Question:
A light is on top of a building that is 15 ft. high. A man, 6 ft. tall, is walking away from the building at the rate of 2 ft/sec. At what rate is the shadow of the man changing when he is 4 ft. away from the building?
My Work:
This is a related rates problem given by the hint "At what rate is the shadow of the man changing..."
I think a similar triangle set up is needed here.
(Height of building)/(height of man) = y/(y - x), where y is the distance from the building to the man and (y - x) is the distance of the man's shadow.
NOTE: SHOULD THE DENOMINATOR BE (y - x) or (y + x)?
What's the difference?
The proportion then becomes
15/6 = y/(y - x)
Solving for y, I get y = (5x/3).
I now must differentiate both sides with
respect to time t, then substitute in what I know for the values of the variables. Since I want the speed of the shadow, I want to find out what dy/dt equals.
d/dt [y] = d/dt [(5x/3)
dy/dt = (dx/dt)(5/3)
I am given that dx/dt = 2 feet per second.
dy/dt = 2(5/3)
dy/dt = 10/3 ft/sec
Can I also write the answer as
dy/dt = 3.33 feet per second?
Is any of this correct?