How do you model a spring and damper in series?

In summary, the conversation is about modeling a spring-mass-damper system and how to represent it when the spring and damper are in series. The question is whether a variable, y, needs to be introduced between the spring and damper. The person asking also shares a diagram and an equation they came up with, but are unsure if it is correct. They also mention the difficulty in solving the equation since y would be an independent variable. They wonder if adding an arbitrary mass at y would help solve the problem. The conversation ends with a clarification that this is not a homework problem, just curiosity.
  • #1
cstoos
62
0
I was wondering about something, and after a quick search through the forums didn't provide an answer I figured I would ask.

So in modeling a spring-mass-damper system, if you have a spring and damper in series, how do you represent that? Do you have to introduce another variable, say y, at a point between the spring and damper?

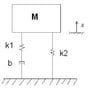
I am attaching a (crude) drawing of a system that I just made up. If I were to model it like this, would that be correct?

M[tex]\ddot{x}[/tex] - b[tex]\dot{y}[/tex] - k1(x-y)-k2x = 0

It seems right, but this would make it impossible to solve, since y would be considered an independent variable. Should I place and arbitrary mass at y so that I can have two DEs?


(P.S. I couldn't get the subscripts to work properly.)
 

Attachments

  • SMDsystem.JPG
    SMDsystem.JPG
    6.4 KB · Views: 1,304
Last edited:
Physics news on Phys.org
  • #2
I have been out of the office for a few days. So, does the lack of response mean that nobody knows or that the solution I presented is accurate?

Edit: This is in no way a homework problem. Just curiousity.
 

Related to How do you model a spring and damper in series?

What is a spring and damper in series?

A spring and damper in series is a mechanical system where a spring and a damper are connected one after the other, with the output of the spring connected to the input of the damper. This arrangement allows for the combined effects of both components to be applied to a system.

What is the purpose of a spring and damper in series?

The purpose of a spring and damper in series is to provide a controlled amount of resistance to a moving object. The spring provides a restoring force, while the damper dissipates energy and reduces the amplitude of oscillations.

How does the stiffness of the spring affect the overall behavior of the system?

The stiffness of the spring affects the overall behavior of the system by determining the amount of force needed to compress or extend the spring. A stiffer spring will result in a higher restoring force and a faster response, while a less stiff spring will result in a lower restoring force and a slower response.

What is the role of damping in a spring and damper system?

The role of damping in a spring and damper system is to dissipate energy and reduce the amplitude of oscillations. Without damping, the system would continue to oscillate indefinitely, leading to a loss of energy and potentially causing damage to the system.

How do the parameters of the spring and damper affect the natural frequency of the system?

The natural frequency of a spring and damper system is affected by the stiffness of the spring and the damping coefficient of the damper. A higher stiffness and lower damping coefficient will result in a higher natural frequency, while a lower stiffness and higher damping coefficient will result in a lower natural frequency.

Similar threads

Automotive Spring and damper on rocker
    • Mechanical Engineering
Replies
2
Views
1K
Engineering Control System mass spring damper
    • Engineering and Comp Sci Homework Help
Replies
0
Views
847
How to solve spring mass damper system manually?
    • Mechanical Engineering
Replies
16
Views
2K
I How Do Eddy Current Dampers Work in Space Applications?
    • Electromagnetism
Replies
4
Views
359
Differential Equations and Damper Curves
    • Mechanical Engineering
Replies
3
Views
1K
I Calculating Recoil Forces in Firearms: How to Choose the Right Damper or Spring
    • Other Physics Topics
Replies
16
Views
3K
I Runge-Kutta 4 w/ some sugar on the top: How to do error approximation?
    • Differential Equations
2
Replies
61
Views
1K
What is the electrical equivalent circuit for this interaction?
    • Engineering and Comp Sci Homework Help
Replies
2
Views
1K
How Do You Calculate the Natural Angular Frequency of a Dual-Spring System?
    • Introductory Physics Homework Help
Replies
5
Views
3K
MATLAB Spring mass impact system in Matlab - How to correct it?
    • MATLAB, Maple, Mathematica, LaTeX
Replies
7
Views
3K

Hot Threads

Recent Insights

Back
Top