- #1
Gunter1977
- 5
- 2
- Homework Statement
- Hobby project PI controller mass spring damper system
- Relevant Equations
- mz_ddot + cdz_dot+kz = External force + Force controller
Hello everybody
I have a question about my control system, and I've included a diagram for reference. In the diagram below, I've illustrated three different control schemes using Simulink. The first scheme represents a PI controller for a mass-spring-damper system, which I understand well. It involves calculating the error between the desired value and feedback, and the units appear to be correctly matched.
My question pertains to the control of the PI controller for position or velocity. In the section highlighted in red within the Simulink diagram, I have made an assumption to ensure unit consistency. However, I'm unsure if this approach is permissible. I have experimented with damping coefficients or stiffness constants as conversion factors, but I'm uncertain whether this is the correct approach or if it is allowed
Could someone provide guidance on how to resolve this issue? Have I gone about it the wrong way, and if so, what would be a more appropriate solution?
Your insights and suggestions would be greatly appreciated. Thank you!
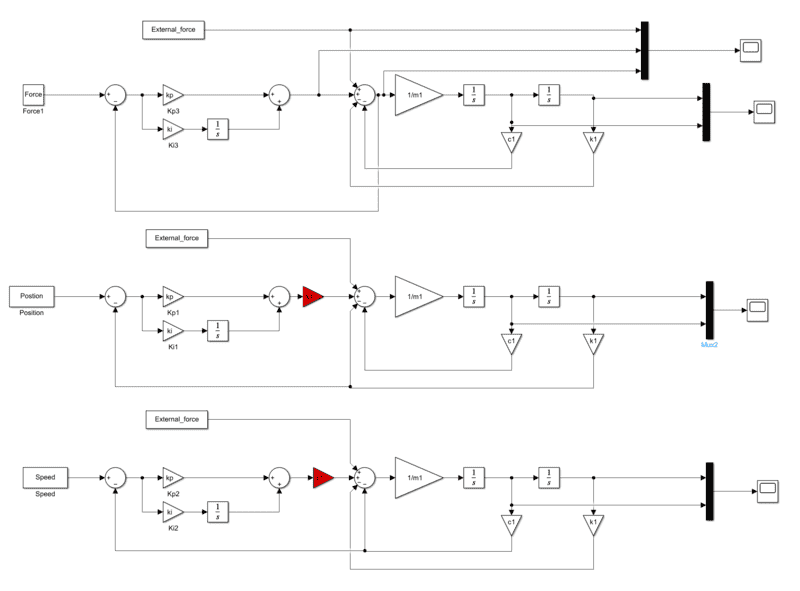
I have a question about my control system, and I've included a diagram for reference. In the diagram below, I've illustrated three different control schemes using Simulink. The first scheme represents a PI controller for a mass-spring-damper system, which I understand well. It involves calculating the error between the desired value and feedback, and the units appear to be correctly matched.
My question pertains to the control of the PI controller for position or velocity. In the section highlighted in red within the Simulink diagram, I have made an assumption to ensure unit consistency. However, I'm unsure if this approach is permissible. I have experimented with damping coefficients or stiffness constants as conversion factors, but I'm uncertain whether this is the correct approach or if it is allowed
Could someone provide guidance on how to resolve this issue? Have I gone about it the wrong way, and if so, what would be a more appropriate solution?
Your insights and suggestions would be greatly appreciated. Thank you!
Last edited by a moderator: