yaro99
- 75
- 0
Homework Statement
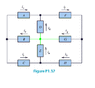
Determine the values of the other currents in Figure P1.37, given that ia = 2 A, ic =−3 A,
ig = 6A,and ih= 1A.
Homework Equations
∑currents entering a node = ∑currents exiting the node
The Attempt at a Solution
I used Kirchoff's Circuit Law on each of the outer nodes:
if = ig + ih = 6 + 1 = 7A
ia + id = if
2 + id = 7
id = 5A
ic + ih= ie
-3 + 1 = ie
ie = -2A
ib = ia + ic = 2 - 3 = -1A
I think I may have went wrong somewhere, because when I apply KCL to one of the inner nodes I get this:
ie + ig = id (?)
-2 + 6 ≠ 5