How Does a Phase Shift Affect the Mach-Zehnder Interferometer?

[WWCY]

Homework Statement

Hi all, I'm working on the following problem and would like some help. Many thanks in advance!

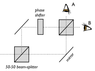
The Figure below presents the Mach-Zehnder interferometer with an additional phase shift element in the upper path.
$$\left( \begin{array}{cc}
e^{i\phi} & 0 \\
0 & 1
\end{array} \right)$$
with $\phi$ as the phase.
a) Calculate the probability that detector A clicks as a function of $\phi$

b) In practice there is always some random phase shift even in the absence of the additional element in the upper path. It comes from misalignment of beam splitters and mirrors. Assume $\phi$ is a uniformly distributed random variable. What is the probability now that detector A clicks as a function of $\phi$?

Homework Equations

The Attempt at a Solution

a) The following vectors define the "right-moving" and "upwards-moving" photon states
$$|r> = (1,0)$$
$$|u> = (0,-1)$$
The initial right mover hits the beam splitter (defined by the matrix below) and the resulting mixed state is
$$

\left( \begin{array}{cc}
\frac{1}{\sqrt{2}} & \frac{1}{\sqrt{2}} \\
-\frac{1}{\sqrt{2}} & \frac{1}{\sqrt{2}}
\end{array} \right)
%
\left( \begin{array}{cc}
1 \\
0
\end{array} \right)
= \frac{1}{\sqrt{2}} \big ( (1,0) + (0,-1) \big)
$$
Both beams then hit mirrors, so I apply the mirror (matrix below) to the mixed state
$$
\left( \begin{array}{cc}
0 & 1 \\
-1 & 0
\end{array} \right)
%
\left( \begin{array}{cc}
1/\sqrt{2} \\
-1/\sqrt{2}
\end{array} \right)
=\frac{1}{\sqrt{2}} \big ( (-1,0) + (0,-1) \big)
$$
Only the top beam hits the phase shifter
$$
\frac{-1}{\sqrt{2}}
\left( \begin{array}{cc}
e^{i\phi} & 0 \\
0 & 1
\end{array} \right)
%
\left( \begin{array}{cc}
1 \\
0
\end{array} \right)
= \frac{-1}{\sqrt{2}} \big ( e^{i\phi},0 \big)
$$
Applying the beam-splitter to both states again yields
$$
\frac{-1}{\sqrt{2}}
\left( \begin{array}{cc}
\frac{1}{\sqrt{2}} & \frac{1}{\sqrt{2}} \\
-\frac{1}{\sqrt{2}} & \frac{1}{\sqrt{2}}
\end{array} \right)
%
\left( \begin{array}{cc}
e^{i\phi} \\
1
\end{array} \right)
= \frac{-1}{2} (e^{i\phi} + 1 \ , 1 - e^{i\phi} )$$

The probability of the detector "a" clicking is thus given by
$$| \frac{1 - e^{i\phi}}{2} |^2 = \frac{1}{2}(1 - \cos\phi )$$

b) I have not formally studied probability theory, but I'm assuming that the phrase "assume $\phi$ is a uniformly distributed random variable" just means that all $\phi$'s are equally likely to occur. I'm also assuming that this phenomenon affects both paths, and to calculate it I'd apply the phase shifter to both "u" and "r" states after they hit the first mirror.

May I know if I have applied concepts correctly? Thanks in advance.

(Spotted some errors, hence the edits)

 

[Gene Naden]

Yes, assume a uniform random variable means that any phase between 0 and 360 degrees is equally likely.

 

[Gene Naden]

Maybe it would be sufficient to only apply the random phase shift to one of the two photon states.

 

[WWCY]

Thank you for your response.

Maybe it would be sufficient to only apply the random phase shift to one of the two photon states.

May I know why this would be sufficient? Would that not mean that the photons taking one path is more "vulnerable" to random phase changes than the other?

Thank you!

 

[Gene Naden]

Oh, sure. I was thinking that what counts is the relative phase between the two photons (causing interference), so that adding a random phase to both of them would not introduce more physics than adding phase to just one of them. Certainly, both paths would be vulnerable to random phase shift.

 

[WWCY]

Oh, sure. I was thinking that what counts is the relative phase between the two photons (causing interference), so that adding a random phase to both of them would not introduce more physics than adding phase to just one of them. Certainly, both paths would be vulnerable to random phase shift.

Thank you for the clarification!

With regards to part c), say I have correctly found that the probability of detector A clicking in part b) to be $P(det A) = \frac{1}{2}(1 - \cos\phi)$ which is bounded between 1 and 0. Does the fact that all $\phi$'s being equally probable mean that $P(det A)$ in part c) is now 0.5, independent of $\phi$?

 

[Gene Naden]

I hope one of the mentors or advisers will weigh in on this. I am having some difficulty interpreting the problem. But your math seems OK. You have indicated that the probability of detection is $\frac{1}{2}(1 - \cos\phi )$. The average of that, assuming $\phi$ is a random variable would be just $\frac{1}{2}$.

 

[WWCY]

I hope one of the mentors or advisers will weigh in on this. I am having some difficulty interpreting the problem. But your math seems OK. You have indicated that the probability of detection is $\frac{1}{2}(1 - \cos\phi )$. The average of that, assuming $\phi$ is a random variable would be just $\frac{1}{2}$.

No worries, thank you very much!

 

[Gene Naden]

I see nobody has picked up your thread, so I will go on with it. Basically, what is bothering me about this problem is that I expect they are trying to get at some kind of interference phenomena, which would produce visible interference fringes. That is what I saw with the interferometer in my optics class. But I don't see how to get that out of your equations. There has to be some kind of distance variable. So these doubts about the problem are why I said I hoped a mentor would come in.