How Does Boyle's Law Explain the Pressure-Volume Relationship of CO2?

[WMDhamnekar]

Robert Boyle's law states that at constant temperature, the pressure of fixed amount ( i-e number of moles n) of gas varies inversely with its volume. Mathematically, it can be written as $p ∝ \frac1V $(at constant T and n) $\Rightarrow p = k_1 \times \frac1V $ where $k_1$is a proportionality constant.

The value of constant $k_1$ depends upon the amount of the gas, temperature of the gas and the units in which p and V are expressed. $p \times V= k_1$

If a fixed amount of gas at constant temperature T occupying volume $V_1$ at pressure $p_1$ undergoes expansion, so that volume becomes $V_2$ and pressure becomes $p_2,$ then according to Boyle’s law : $p_1 \times V_1 = p_2 \times V_2=$ constant $\Rightarrow \frac{p_1}{p_2} = \frac{V_2}{V_1}.$

It should be noted that volume V of the gas doubles, if pressure is halved.

The following table 5.1 gives effect of pressure on volume of 0.09 mol of CO₂ at 300 K. but i didn't understand these calculated values given in the second column. I also didn't understand the meanings of headings given to each column. If any member can explain me how the values in the second column is computed, may answer to this question.

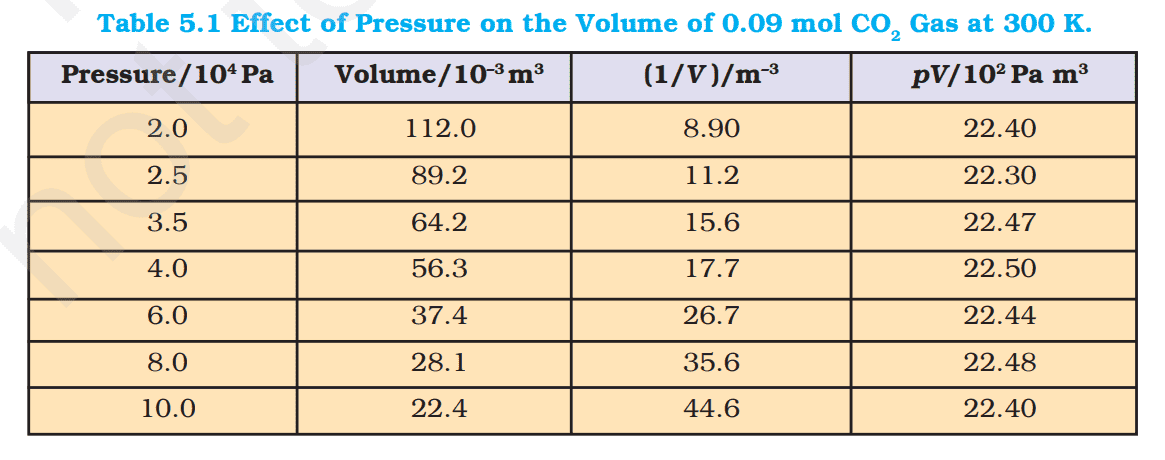My understanding:

$V= \frac{nRT}{p}\tag {1}$ where n, R, T, p are constants. n stands for number of moles, R is gas constant, T is temperature and p is pressure.

Putting the given values in this equation (1),we get 11.2 liters =$\frac {0.09 mol \times 8,314 J k^{-1} mol^{-1}\times 300 K }{20000 Pa}$

But in the second column, it is $112 \times 10^{-3} m^3= 112 $ liters . How is that? Where i am wrong?Can we compute the volume of $CO_2$ in another way? For example, by using this known information that one mole of $CO_2$ molecules features a volume of 22.414 liters at standard T and p. So, 0.09 mol of $CO_2$ features a volume of $0.09 \times 22.414= 2.01726 $ liters at STP.

 

[I like Serena]

Which table are we talking about?
Otherwise I can only guess why it would show $112\times 10^{-3}\,m^3$.

Either way, your substitution in the ideal gas law (equation 1) has $p=20\,000\,Pa$, which is not standard pressure.
If instead we substitute the STP values $p_0=100\,000\,Pa$ and $T_0=273.15\,K$, we find:
$$\frac {0.09\, mol \times 8.314\, J K^{-1} mol^{-1}\times 273.15\, K }{100\,000\, Pa} = 2.04\, L$$
which agrees with what you found using the molar volume at STP.
Note that the ideal gas law predicts a slightly higher value (1%), which is because a real gas is slightly more cohesive than an ideal gas.

 

[WMDhamnekar]

Which table are we talking about?
Otherwise I can only guess why it would show $112\times 10^{-3}\,m^3$.

Either way, your substitution in the ideal gas law (equation 1) has $p=20\,000\,Pa$, which is not standard pressure.
If instead we substitute the STP values $p_0=100\,000\,Pa$ and $T_0=273.15\,K$, we find:
$$\frac {0.09\, mol \times 8.314\, J K^{-1} mol^{-1}\times 273.15\, K }{100\,000\, Pa} = 2.04\, L$$
which agrees with what you found using the molar volume at STP.
Note that the ideal gas law predicts a slightly higher value (1%), which is because a real gas is slightly more cohesive than an ideal gas.

Hello,

Sorry. I forgot to add the table. Now, i have added it to my question.

 

[I like Serena]

It looks as a mistake in the table. I believe the unit in the pressure column should be $10^3\,Pa$. Then the other 3 columns have the correct values.
We can verify with either molar volume or ideal gas law at $T=300\,K$, or we can look it up with an online calculator or table.