How Does Current Direction and Charge Flow in a Solenoid-Wire System?

[Eitan Levy]

Homework Statement

[/B]
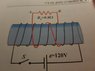
A solenoid is not connected to an ideal voltage source.
Its radius is 0.05m, it has 800 loops per meter and its resistance is 0.2Ω. ε=120V.
Around the solenoid we bind two loops of a wire. The loops are attached to a resistor with the resistance of 0.8Ω.
Suddenly, we connect the voltage source.
What is the direction of the current in the wire?
What is the total amount of charge that flows through the resistor?

Homework Equations

B=μ₀nI.
ε=IR

The Attempt at a Solution

I succesfully calculated that the change in the flux would be -9.47*10^-3Wb.
Regarding the first question, I thought that inside the solenoid a magnetic field is created pointing to the right (but I am really not sure about it). So the wire will have to create a magnetic flux pointing to the left, and that in order to do so the current will have to flow from A to B.
Regarding the second question, I simply don't understand how can we know when current will not flow anymore in the wire? When does it stop and why?

 

[TSny]

Regarding the first question, I thought that inside the solenoid a magnetic field is created pointing to the right (but I am really not sure about it).

Yes. If you want to check your understanding of this, please explain how you deduced the direction of the field of the solenoid.

So the wire will have to create a magnetic flux pointing to the left, and that in order to do so the current will have to flow from A to B.

Yes.

Regarding the second question, I simply don't understand how can we know when current will not flow anymore in the wire? When does it stop and why?

It is interesting that you don't need to know the details of how the current changes with time. Hint: Integrate Faraday's law of induction.

 

[Eitan Levy]

Yes. If you want to check your understanding of this, please explain how you deduced the direction of the field of the solenoid.

Yes.
It is interesting that you don't need to know the details of how the current changes with time. Hint: Integrate Faraday's law of induction.

I reached this conclusion by rotating the solenoid by 90 degrees and then using the second right hand rule, definitely not the most simple way.
Okay, so I had this idea:
ε=N*Δ∅/Δt
ΔQ/Δt*R=N*Δ∅/Δt
ΔQ=N*Δ∅/R.
I thought that because we have 2 loops I need to multiply by N (by 2). However according to the book it's wrong (The correct answer is when you don't multiply by N), why?
Perhaps it's because I already multiplied by 2 when I calculated the flux?

 

[TSny]

Did you already multiply by 2 in finding the value of the change in flux that you stated in your first post?

 

[Eitan Levy]

Did you already multiply by 2 in finding the value of the change in flux that you stated in your first post?

Yes, I figured that was the problem.