How Does Magnet Position Affect EMF in a Coiled Wire System?

[timetraveller123]

sorry for the very late reply my exams are starting soon and i have to focus on my academics hope you understand

i am having some problems

so using the relation

dΦ/dt = dΦ/dx *dx/dt
dx/dt = v
i decided to express v of x
so it is
v = w√(A² - x^2)
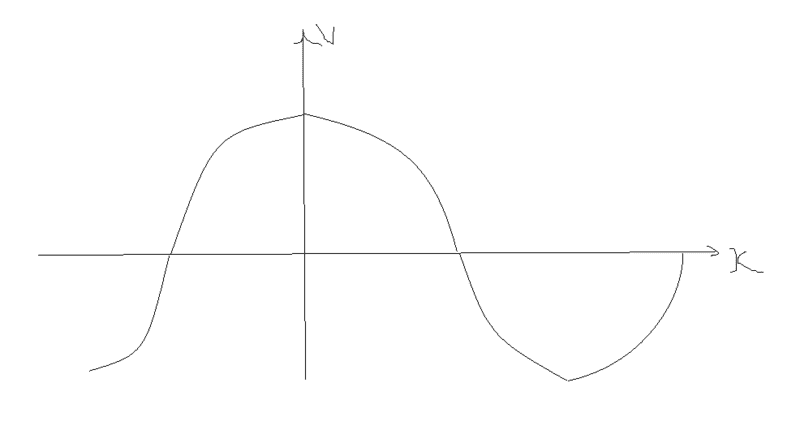
so the graphs looked like this

hence the final dΦ/dt turned to look like this

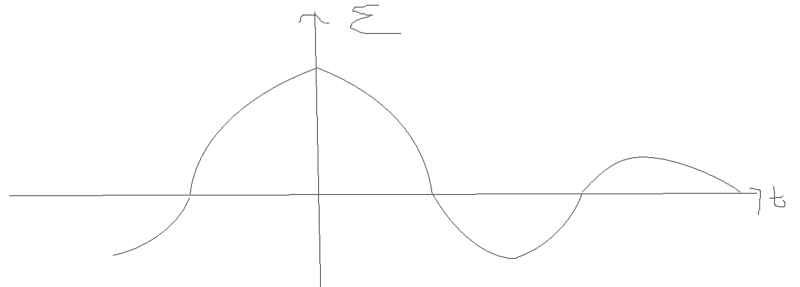
in other words a damped oscillation
but i am not understanding this
there is a certain level of symetry in the problem in that after every oscillation the emf should be the same at the same position as the before oscillation but in this sketch it seems to suggest that the emf would never reach the same value again as time progresses

 

[TSny]

I'm not following what you did here. You have $\varepsilon = - \frac{d \Phi}{dt} = -\frac{d \Phi}{dx} \frac{dx}{dt}$.

From post #21 you have that $\frac{d \Phi}{dx}$ is linear in $x$ with a negative slope (for small oscillations). So, it can be written $\frac{d \Phi}{dx} = -b x$, where $b$ is some positive number. I don't see a way to determine a value for $b$ from the data given in the problem.

So, $\varepsilon = -\frac{d \Phi}{dx} \frac{dx}{dt} = bxv$. Or, as a function of time, you have $\varepsilon (t)= bx(t)v(t)$. You already have expressions for $v(t)$ and $x(t)$.

 

[timetraveller123]

oh sorry i used phi(x) instead of dphi/dx i will try again
thanks for the fast reply

 

[timetraveller123]

ok since v(t) is cosine and x(t) is -sine they both have same frequencies
v*x = -1/2sin 2w scaled uo by a factor of b

 

[TSny]

Yes. The frequency of the emf is twice the frequency of the oscillation of the magnet.

 

[timetraveller123]

ok now the last part of the question there are 5 options i eliminated two of them

qn)which of the following is true?

1)the magnitude of the emf is maximum only when the force is zero

2)the magnitude of the force is zero only when the magnitude of the force is maximum.

3)none of the above

which one is it both seem to be correct