Thanks you everybody!
@Delta2, I read your post, very helpful! So, let's see if I understood it properly. Consider the image below of a wire conducting a current. There is a voltage difference V in the wire so that the current is to the right and there is also a magnetic field pointing into the paper:
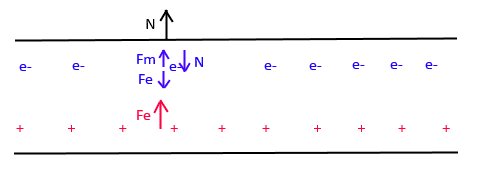
As the wire is a conductor, there are a lot of free electrons in it. These electrons move freely, so I will consider them to be a separate body. The electrons are the only charges who are actually moving, so only on them there is a magnetic force upwards ##Fm=qvB##. The Hall effect will make the electrons go up and a positive vacancy be created in the bottom. As the positive vacancy is not moving, and is not free, there is no magnetic force being made on it, and we will also consider it to be part of the wire body. The Hall force created is equal to ##Fe##. By the equilibrium of forces in the electron (considering electron mass is almost zero) ##N=Fm-Fe##, so the net force in the wire body is ##N+Fe=Fm##. Until now, did I understand everything properly?
Ok, now my real problem is when I try to see who is doing work. I understand that, if we consider the above forces to be the only forces acting in the wire, there will be an acceleration upwards and a net work being done. By what I think I understood, the force doing the work is N? What is the nature of that force?
Also, when the electrons move upwards due to Hall effect, it seems to be a work being done on them (in this case by the magnetic force that is upwards and the trajectories that seem to be upwards too), I can think of an explanation where the electrons move in a circular path as when we study a single charged particle in a magnetic field, and the work is zero because the magnetic force is acting as centripetal (is it true?).
What when the electrons get to their final vertical position relative to the wire, in the top of it, and the wire starts to accelerate upwards because of N? The electrons will also accelerate upwards. Will the magnetic force on the electrons continue to act as centripetal? How? In that case, what will be the trajectory of the wire (will it accelerate upwards in a straight line or will the wire starts to rotate)?
I'm asking this because the velocity of the electrons in the vertical plane will be much higher than the drift velocity in the horizontal plane. So there will be another "Hall effect" on the electrons where magnetic field will produce a force to thhe right. If the wire accelerate upwards in a straight line this effect will effectively reduce V. We could calculate the force acting on the electrons because of V. This would be ##Ve/d## where d in the length of the wire. The magnetic force acting on the electrons when they are accelerating upwards is evB. If we consider V=1V, d=10m, B=0,01T and v=10m/s (I think these values can happen in real life) we would zero net force effectively stopping the current. Is this true?