freshcoast
- 185
- 1
1. Problem statement
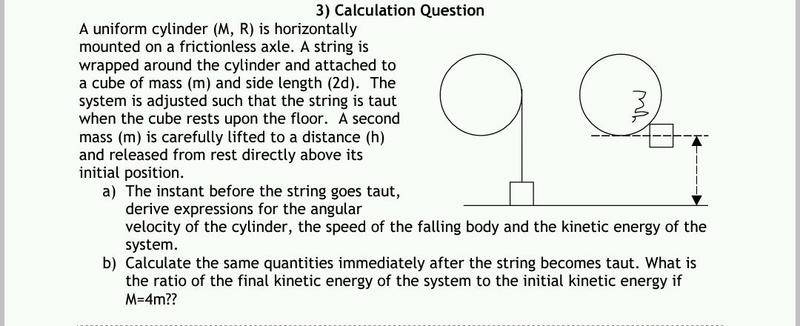
2. Related equations
I = bmr^2
Energy equations (linear and rotational)
3. Attempt
Part a)
I know that the distance or height traveled by the box is [h - d] because center of the mass of box is just d. Initial kinetic energy of the box and cylinder is 0 and if only conservative forces are at play, I applied the conservation of energy laws and I am just left with potential energy = KF[translational] KF[rotational]. I also know that v = rw. So substituting in the correct variables i have come up with the general solution for the velocity of the box as its dropping, the rotational speed of the cylinder and the energy of the system.
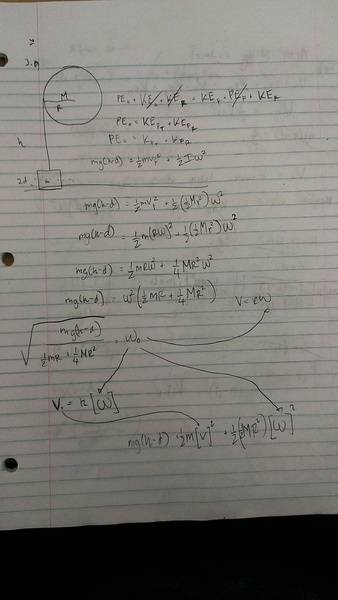
Part b)
Assuming if part a is correct, and knowing that the system is a perfectly inelastic collision I can find the new rotational speed (wf) by using conservation of momentum which looks like
Mbvb + Iwo = Iwf
For the initial conditions, I can just use the (wo) from part a.
And so to compare the ratio from initial to final I just used energy conservation laws again but the kinetic final for box is 0 since it is at rest and I just used kinetic rotational over potential energy. But the answer is messy so before I try all that I just want to make sure I'm on the right path.
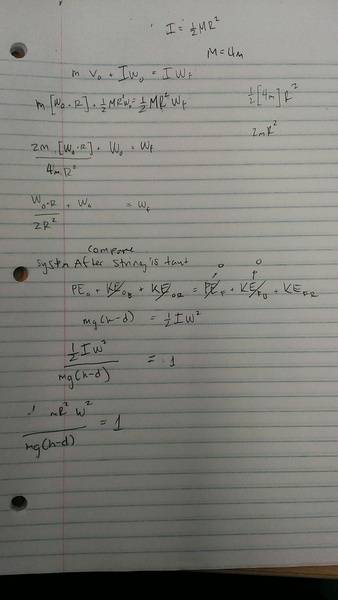
2. Related equations
I = bmr^2
Energy equations (linear and rotational)
3. Attempt
Part a)
I know that the distance or height traveled by the box is [h - d] because center of the mass of box is just d. Initial kinetic energy of the box and cylinder is 0 and if only conservative forces are at play, I applied the conservation of energy laws and I am just left with potential energy = KF[translational] KF[rotational]. I also know that v = rw. So substituting in the correct variables i have come up with the general solution for the velocity of the box as its dropping, the rotational speed of the cylinder and the energy of the system.
Part b)
Assuming if part a is correct, and knowing that the system is a perfectly inelastic collision I can find the new rotational speed (wf) by using conservation of momentum which looks like
Mbvb + Iwo = Iwf
For the initial conditions, I can just use the (wo) from part a.
And so to compare the ratio from initial to final I just used energy conservation laws again but the kinetic final for box is 0 since it is at rest and I just used kinetic rotational over potential energy. But the answer is messy so before I try all that I just want to make sure I'm on the right path.