How does the addition of a lift affect the forces on a space elevator?

[sander2798]

Hello everyone,

I am trying to find out how space elevators work, but there is one think I can't figure out.

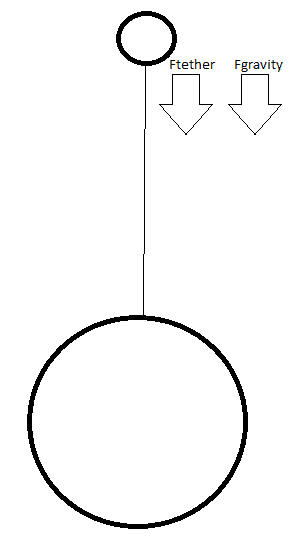
Normally, the forces on the countermass and it's tether will be as following, assuming you neglect the gravity on the tether.

But now, I put the lift somewhere on the cable (below geostationary orbit), like this.

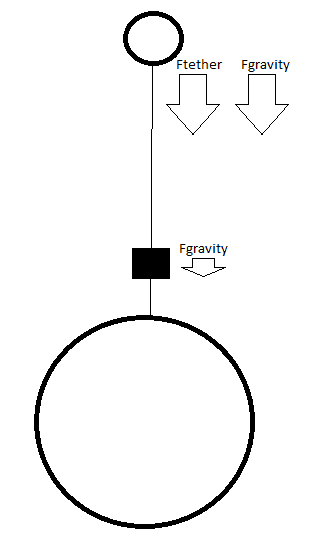
The total forces added up are more than the centripetal force needed to keep the counter mass in orbit, right? So how is it that the countermass doesn't come falling down?

Thanks in advance,
Sander.

 

[Dale]

So how is it that the countermass doesn't come falling down?

Analyzed from an inertial frame it is falling down. Always. It is just going sideways very fast too, which keeps the distance from decreasing despite the fact that it is being pulled strongly down.

This may be easier to understand in the rotating reference frame. In that frame it is kept up by the centrifugal force.

 

[mfb]

The total forces added up are more than the centripetal force needed to keep the counter mass in orbit, right?

There is some safety factor included in the mass and position of the counterweight: there is constant tension. Imagine a permanent load attached to the cable on the ground. Moving a part of this load up doesn't change the force balance. It just reduces tension below the weight.

 

[sander2798]

Analyzed from an inertial frame it is falling down. Always. It is just going sideways very fast too, which keeps the distance from decreasing despite the fact that it is being pulled strongly down.

This !ay be easier to understand in the rotating reference frame. In that frame it is kept up by the centrifugal force.

With "falling down" I actually meant "getting closer to the earth", so I still don't understand it, but thanks for your response. :P

 

[sander2798]

There is some safety factor included in the mass and position of the counterweight: there is constant tension. Imagine a permanent load attached to the cable on the ground. Moving a part of this load up doesn't change the force balance.

Yes, but assume you don't have any mass on the cable. The tension is a constant force, right? Adding the gravity of the counterweight to this should be equal to the centripetal force. So if you'd put a mass on this tether, the total forces pulling the countermass towards the Earth will be bigger than the needed centripetal force for a circular movement. As far as I know the result of this will be that the countermass will start coming closer to the Earth and start falling as soon as it passes geostationary orbit.

It just reduces tension below the weight.

It indeed reduces the tensions below the weight, but don't the tensions above the weight become bigger as a result of that?

Thanks a lot for your response!

 

[russ_watters]

With "falling down" I actually meant "getting closer to the earth", so I still don't understand it, but thanks for your response. :P

Well, your first diagram shows two forces, both pulling in the same direction. You mention the centripetal force but you didn't show it.

That said, in your second diagram, the magnitudes of the forces don't seem to have changed. So the anchor's disposition hasn't changed.

I think perhaps if you make your diagram more detailed it will become clearer.

 

[russ_watters]

Yes, but assume you don't have any mass on the cable. The tension is a constant force, right? Adding the gravity of the counterweight to this should be equal to the centripetal force. So if you'd put a mass on this tether, the total forces pulling the countermass towards the Earth will be bigger than the needed centripetal force for a circular movement. As far as I know the result of this will be that the countermass will start coming closer to the Earth and start falling as soon as it passes geostationary orbit.

Can the cable maintain its tension if the moon moves closer to earth? And from the other way: if, for example, you decide to add some more centripetal force, what does the cable do?

 

[DrStupid]

It indeed reduces the tensions below the weight, but don't the tensions above the weight become bigger as a result of that?

Only if you overload the elevator. This would happen if the additional weight exceeds the initial tension. Within the safe range of operation the additional weight and the reduced tension cancel each other out.

 

[mfb]

Yes, but assume you don't have any mass on the cable. The tension is a constant force, right? Adding the gravity of the counterweight to this should be equal to the centripetal force.

It is.

So if you'd put a mass on this tether, the total forces pulling the countermass towards the Earth will be bigger than the needed centripetal force for a circular movement.

No, adding a mass does not change the upper part of the elevator at all. Tension there stays the same. The mass is "supported" by the reduced tension in the cable below the mass. The difference in tension (purely from the reduction below) balances the mass.

 

[sander2798]

It is.No, adding a mass does not change the upper part of the elevator at all. Tension there stays the same. The mass is "supported" by the reduced tension in the cable below the mass. The difference in tension (purely from the reduction below) balances the mass.

That was exactly what I didnt understand. Good explanation, thanks a lot!