How Does the Flow Equation Apply in Higher Dimensional Phase Spaces?

[Kashmir]

We are in phase space of $6N$ dimensions. Each point $\mathbf r$ in this space has $6N$ coordinates.

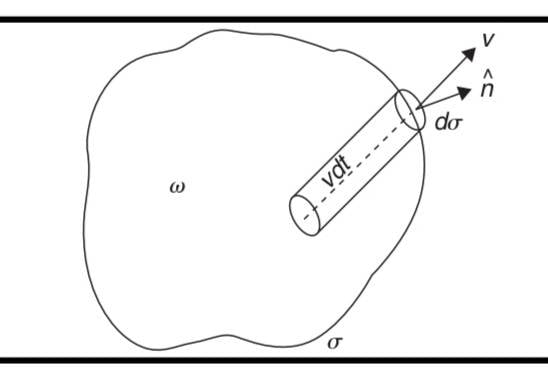
Pathria writes "Consider an arbitrary "volume" $\omega$ in the relevant region of the phase space and let the "surface" enclosing this volume be denoted by $\sigma$ then the net rate at which the representative points "flow" out of $\omega$ (across the bounding surface $\sigma$ ) is given by
$\int \rho \boldsymbol{v} \cdot \hat{\boldsymbol{n}} d \sigma$"

Where $\boldsymbol{v}$ is velocity and $\rho$ is number density function

I can understand why the equation is true in 3D however in higher dimensions I'm not sure why it holds . Please help me

 

[DrClaude]

Could you see why it would hold in 2D, where the two dimensions would be $p_x$ and $x$?

(Note that $\mathbf{v}$ here is a generalization of velocity, not the actual velocity of a particle.)

 

[Kashmir]

Could you see why it would hold in 2D, where the two dimensions would be $p_x$ and $x$?

(Note that $\mathbf{v}$ here is a generalization of velocity, not the actual velocity of a particle.)

No sir, I cannot.

 

[DrClaude]

But you can see how it works in 3D?

 

[Kashmir]

But you can see how it works in 3D?

I had forgotten that we were talking about genralised velocities. I had in mind a 3D spatial velocity vector.

 

[DrClaude]

I had forgotten that we were talking about genralised velocities. I had in mind a 3D spatial velocity vector.

You have to generalize to the time derivative of the coordinates, but the principle is the same.

 

[Kashmir]

You have to generalize to the time derivative of the coordinates, but the principle is the same.

I understand that we have a generalized velocity vector now, however I don't get how the same principle would apply?

Is it that it's proof is advanced so the author has skipped it?

 

[DrClaude]

I understand that we have a generalized velocity vector now, however I don't get how the same principle would apply?

The same conservation principles apply, that points in phase space can only move around, they never get created or destroyed.

Is it that it's proof is advanced so the author has skipped it?

Don't take this the wrong way, but I would say the author doesn't give a proof because they consider this trivial. Again, just think in terms of basic conservation principles.