How does the thickness of a clamp affect its ability to transmit torque?

[Andrea Vironda]

Good morning sirs,
let's imagine a cylinder, surrounded on 360° by a coating of the same shape. I can close the 2 half using 2 bolt screws.
what's the maximun transmittable torque?
here's a scheme:

i would to consider the sum of forces as a normal force on the top of the cylinder, producing a tangential force, and so a torque, proportional to the friction coefficient.
My doubt is: why do the total surface is not taken into consideration? is only a section enought?

 

[jrmichler]

If the two clamping pieces have a bore diameter slightly larger than the shaft, and are rigid enough to hold their shape under the clamping forces, then you can calculate the maximum torque from the total clamping force times the shaft radius times the friction coefficient. The width of the clamping piece (dimension along the length of the shaft) does not matter. It only needs to be wide enough to hold the bolt, or bolts if four or more bolts are needed.

If, however, the clamping pieces are thin enough to conform to the shaft, then it is analyzed as a thin walled pressure vessel. The total clamping force is 2F. The pressure (normal force on the shaft) is calculated from 2F = 2*R*P, where R is the shaft radius. Solve for P, and multiply by the circumference of the shaft to get total normal force. Note that I did not include the width of the clamping pieces because it drops out of the equation. Total normal force times shaft radius times friction coefficient gives you the maximum torque. It will be larger than the maximum torque with rigid clamping pieces.

When the clamping piece conforms to the shaft, one bolt gives the same maximum torque as two bolts. If you have difficulty visualizing that, cut the clamping piece on a plane through the center of the shaft, and make a free body diagram.

I have used thin clamps in many cases where it was necessary to transmit large torques reliably. They work well, especially in cases involving high speed reversing torques.

 

[Andrea Vironda]

Why do the width is not important? if i have a 1 km cylinder i think i have to put a lot of effort more

 

[jrmichler]

Go through the calculations for two different widths, say one inch and 10 inches (or 1 cm and 1 meter). If the total clamping force is the same, the maximum torque without slipping will be the same. Remember that the coefficient of friction is independent of surface pressure. With your Master's degree in M.E., the calculations should be well within your abilities.

Hint: Be very careful to get the free body diagram correct.

 

[MechE_UT_13]

Hi jrmichler,

I am working on designing a clamp to act as a break on a shaft of a large industrial fan while we work on the equipment. I have seen you discussions on such. Can you show me your calculations on how you modified the thin wall pressure vessel equation. I am having trouble filling in that blank. Thank you.

MechE

 

[jrmichler]

Don't take this the wrong way, but when you brake a brake, something slows down, while when you break a brake it does not.

The top left sketch in the following sketch represents a thin wall pressure vessel. The top right sketch is the free body diagram for a thin wall pressure vessel. The radius is R, the pressure is P, the length (or width) is W, and the force in each wall is F. The total force 2F is the pressure times the projected (not the actual) area, so 2F = 2R*P*W. Solving for P, we get P = F / (R*W).

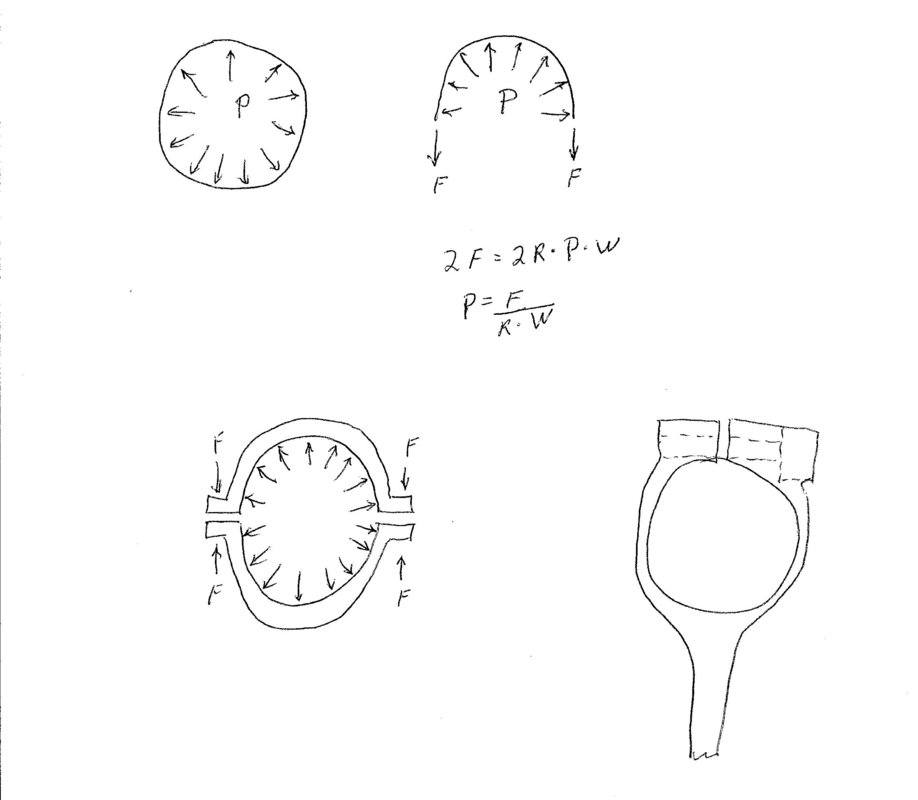
The lower left sketch is the same as the top right, except it is a simplified representation of a thin wall bolted clamp, where the bolt force is F. Thin is relative. In clamp fits, thin means that a small (definitely less than 10%) fraction of the clamp force is needed to elastically deform the clamp to fit to the shaft. If the clamp is very thin (such as in a hose clamp), the initial fit can be very loose. A 2" hose clamp will easily pull into fit a 1" hose. If the clamp is thicker, the initial fit may have as little as 0.001" clearance. If you can tighten the bolt(s) finger tight and feel the clamp gripping the shaft, you are good. If finger tight does not make it grip the shaft, you may need to redesign the clamp or do further analysis using FEA or both.

When the force to get the clamp in proper contact with the shaft is small, then we can assume that 100% of the bolt force is going to clamping force, and none of the bolt force is pulling the clamp up to the shaft. Then we can use the equation from above: P = F / (R*W), where P is the pressure between the clamp and the shaft.
The total normal force between the clamp and the shaft is pressure times area, so
Normal Force = (F / (R*W)) * 2*PI*W.

The torque is the Normal Force times the radius times the coefficient of friction:
Torque = (F / (R*W)) * 2*PI*W * R * mu.
Cancel and rearrange: Torque = 2*PI*F*mu*R.

The bottom right sketch shows a typical implementation of a clamp fit. Note that, when the clamp can flex to fit the shaft, one bolt has exactly the same total clamp force and friction torque as two bolts on opposite sides. If you need to convince yourself of this, look at the bottom left sketch, and replace one of the bolts with a continuation of the clamp. Then cut it and do an FBD.

Note the dashed lines in the bottom right sketch that represent the bolt hole. The bolt body is very close to the shaft. These type of components work best when the bolt is as close as possible to the shaft. It is normal for the bolt hole to break out into the clamping surface.

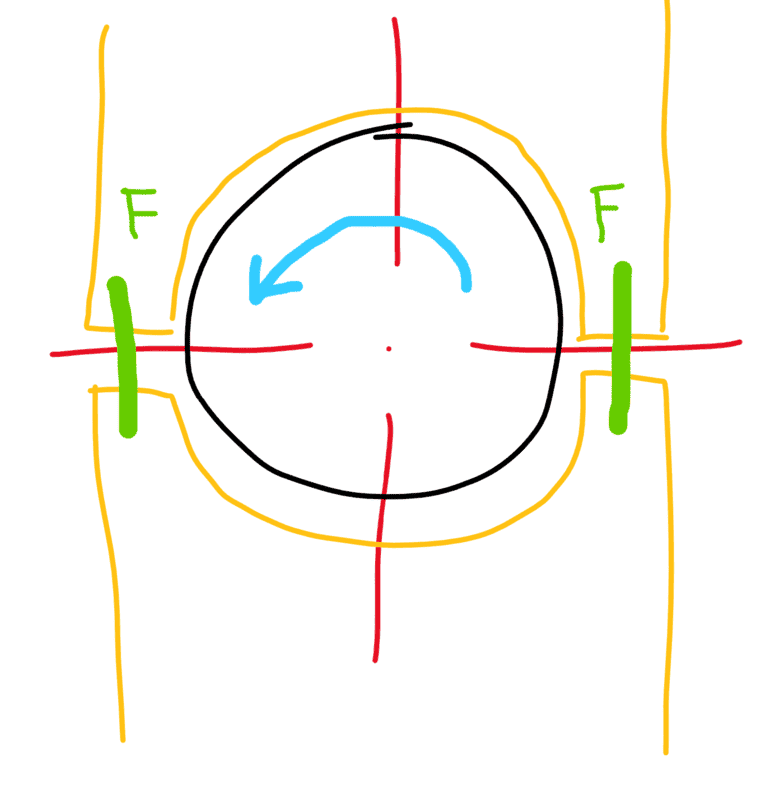
One way to mount a brake disk to a shaft is by using a shaft collar:

Tap holes in the side of the shaft collar, mount it to the shaft, then bolt the brake disk to the shaft collar. If purchased shaft collar is not suitable, you may need to design your own. Be sure to calculate both the slip torque and the bolted joint for the disk. And remember your safety factors.

Note that if the clamp is too rigid, and clearance too large, to conform to the shaft, then the slip torque is only 4*F*mu*R.