russ_watters
Mentor
- 23,829
- 11,306
In order for the plane to go from 0-100 kts it has to accelerate. My point in pointing this out is that you are mixing together two different scenarios as if they were part of the same scenario. An airplane sitting stationary on a runway and an airplane flying at 100 kts are two completely different scenarios.thetexan said:Who said anything about an accelerating airplane? At a steady 100kt velocity there is no accelerating airplane.
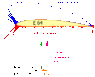
Of course Bernoulli's principle applies in both surfaces. But Bernoulli's principle applies to flows that both speed up and slow down. On the top surface it speeds up and on the bottom it slows down. Here's a diagram indicating the resulting pressure profile:I have studied many diagrams and now understand the dynamic/static relationship.
There is an acceleration then deceleration of the flow over the wings curved surface...and the same over the wings curves surface under the wing. A gentler curve but a curve none the less. If Bernouli applies above the wing it does so also under the wing and that IS a fact.
As you can see, the red arrows indicate pressure above ambient on the bottom of the airfoil.
Static pressure change. It can be an increase (on the bottom surface) or reduction (on the top).So, as I understand it the static pressure reduction is what we are interested in when considering the difference between upper and lower wing pressures that produce lift, is that right?
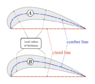
Here's a diagram with a velocity profile:
https://www.mh-aerotools.de/airfoils/velocitydistributions.htm
Let us follow the flow from the stagnation point, along both sides of the Eppler E 64 airfoil at 2º angle of attack, as shown above:
- Starting from v/
=0 in the stagnation point, the velocity v increases rapidly to 1.38 times the velocity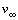 of the onset flow near the location x/c=0.1. Further downstream the velocity gradually decreases and reaches at the trailing edge approximately 85% of the free stream velocity
of the onset flow near the location x/c=0.1. Further downstream the velocity gradually decreases and reaches at the trailing edge approximately 85% of the free stream velocity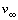 .
.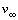
- The velocity of the flow on the lower surface looks similar, but its level is considerably lower. In this example, it always stays below the free stream velocity.