How Is Acceleration Calculated in a Basic Table Pulley System?

[gummybeargirl]

Homework Statement

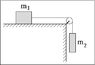
Mass m1 = 14.9 kg is on a horizontal surface. Mass m2 = 7.48 kg hangs freely on a rope which is attached to the first mass. The coefficient of static friction between m1 and the horizontal surface is μs = 0.571, while the coefficient of kinetic friction is μk = 0.105. If the system is in motion with m1 moving to the left, then what will be the magnitude of the system's acceleration? Consider the pulley to be massless and frictionless.

Homework Equations

∑F = ma

The Attempt at a Solution

For m1: T-μs*m1*g = m1*a
For m2: -T-m2*g = m2*a

Then i substitute → -m2*a-m2*g-μ*m1*g = m1*a
When i plug in my numbers i get the acceleration to be 2.59 m/s^2, which i correct if the system where moving right. I am not sure where i am going wrong or how to get the acceleration going left.

 

[Doc Al]

For m1: T-μs*m1*g = m1*a

Since it's moving, you need kinetic friction.

For m2: -T-m2*g = m2*a

You have a sign problem. Tension and weight act in different directions.

A diagram would have been nice! (Or at least a description of which mass is on the left.)

 

[gummybeargirl]

Sorry i totally forgot to include the diagram. I hope this will help, i am still a little confused as to why i am not getting the correct answer.
I tried fixing some of those errors and got two equations:
M1: T+μk*m1*g = m1*a
M2: T-m2*g = m2*a
I combined these and got:
m2*a + m2*g + μk*m1*g = m1*a → giving me an answer of 11.96 m/s^2, which is incorrect.

 

[Doc Al]

I tried fixing some of those errors and got two equations:
M1: T+μk*m1*g = m1*a

Good.

M2: T-m2*g = m2*a

You still have a sign error, but a different one. Note that in your first equation, you took "a" as being to the right. If m1 accelerates to the right, then m2 must accelerate downward.

You're almost there.

 

[gummybeargirl]

Since it's moving, you need kinetic friction.


You have a sign problem. Tension and weight act in different directions.

A diagram would have been nice! (Or at least a description of which mass is on the left.)

Good.


You still have a sign error, but a different one. Note that in your first equation, you took "a" as being to the right. If m1 accelerates to the right, then m2 must accelerate downward.

You're almost there.

Thank you so much! I fixed my signs and was able to get the correct answer. Thanks for walking me through the entire issue.

 

[bvishnu9]

Whenever you have a situation like this, first make a FBD (Free Body Diagram). It indicates the forces and their directions acting on the objects.

 

[Crush1986]

Out of curiosity was the correct answer 3.96 m/s^2 to the right? I'd type out my symbolic answer but I'm on my phone.