How Is Heat Calculated in a Diesel Cycle Using Volumes and Temperatures?

[cloud809]

1. Ideal gas cycle - diesel engine cycle. You begin at some volume V₁. Perform an adiabatic compression to V₂. Perform an expansion to V₃ at constant pressure. Next, perform an adiabatic expansion to V₄, Last, it moves back to V₁ at a fixed volume, while decreasing temperature back to original starting point.

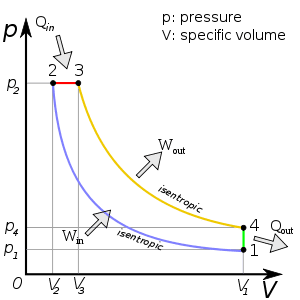
NOTE: Ignore "specific volume," and just consider it to be generic "volume" for my case.

Find Q_in and Q_out in terms of V₁, V₂, V₃, and T₁.

--

2. 1st law: ΔU = W + Q, where W = -∫PdV

We're told that the 1st law is the assumed starting point for this problem.

--

3. For Q_in, I began that ΔU = 0 for 2→3, so -W_2→3=Q_in. This yielded

Q_in=- (-∫₂³PdV)

or Q_in = P(V₃-V₂).

Am I right to assume that ΔU=0 for this 2→3 phase? I can't find how to incorporate V₁ and T₁ if my method was ok.

--

Then, for Q_out, I noted that W = 0 for 4→1, so ΔU_4→1=Q_out.

So, I found that ΔU = Nk(f/2)_BΔT, or Q_out = Nk_B(f/2)(T₁-T₄). And again, I'm running into the same issue of not filling the parameters of the original question.

 

[cloud809]

One thing I just realized is that for 2→3, I shouldn't have said ΔU = 0. Instead, I should have set up Q_in as:

Q_in = ΔU - W, where

ΔU = Nk_B(f/2)ΔT

ΔU = Nk_B(f/2)[(PV₃-PV₂)/Nk_B]

and W is still W=-P(V₃-v₂)

so, once simplified (Q_in = ΔU - W), Q_in=P[V₃((f/2)+1)-V₂((f/2)+1)].

This still doesn't put it in terms of V₁, V₂, V₃, T₁ however.

 

[TSny]

so, once simplified (Q_in = ΔU - W), Q_in=P[V₃((f/2)+1)-V₂((f/2)+1)].

This still doesn't put it in terms of V₁, V₂, V₃, T₁ however.

Try to express P in terms of volume and temperature. Don't forget the adiabatic law $TV^{\gamma-1} =$ const.

 

[cloud809]

Thanks for the reply TSny.
I've considered something similar and figured it out I believe.
I used P₁V₁^1+f/2=P₂V₂^1+f/2, solved for P₂, and substituted that into my Q_in equation. And since there was still a P₁ in there, I used the PV=Nk_BT for P₁ to put it in terms of T₁. Now my Q_in satisfies all 4 variables (V1, V2, V3, T1).

Now to spend a bit more time and figure out Q_out...

 

[TSny]

Sounds good!