- #1
Pull and Twist
- 48
- 0
One big coincidence of thermodynamics is that automobiles are usually powered by an Otto cycle This cycle consists of an adiabatic compression (the cylinder compresses), isochoric compression (the fuel ignites, increasing the temperature in too short a time for the piston to move), adiabatic expansion (the cylinder expands), and isochoric expansion (exhaust gas let out, fresh air and fuel let in.)
In a particular engine, a starts by taking in 1000cm3 of air (p=1.2kg/m3). Next, an amount of fuel is added equivalent to 1% of the mass of the air in the piston (since gasoline is composed of large molecules, assume that this does not affect the pressure in the piston). The piston is then compressed to a volume of 100cm3. This compression can be assumed to be adiabatic with PV1.3 being constant. Next, the fuel is ignited, releasing an energy of 45000J for every gram of fuel in the form of heat, while the piston stays at constant volume. You may assume that the heat capacity at constant volume for this gas is 800J/kg*K. After combustion, the piston expands back to the original volume of 1000cm3 adiabatically, and the gasses are released.
1) What is the work required to compress the gas during compression, work done by the gas during the expansion, and total work done during the cycle.?
2) How much heat is added to the system during the combustion stage?
Hint: You may want to answer questions 1&2 together in the form of a U table
3) What is the efficiency of this particular cycle?
4) What is the temperature of the released gas?
Equations we have learned in this section...
PV=NKBT
W=PV
E=Q - W
E=CvT
Was told to utilize google for any other equations or constants that may be useful...
This is how I started working stuff out... but have no idea what I'm actually doing.
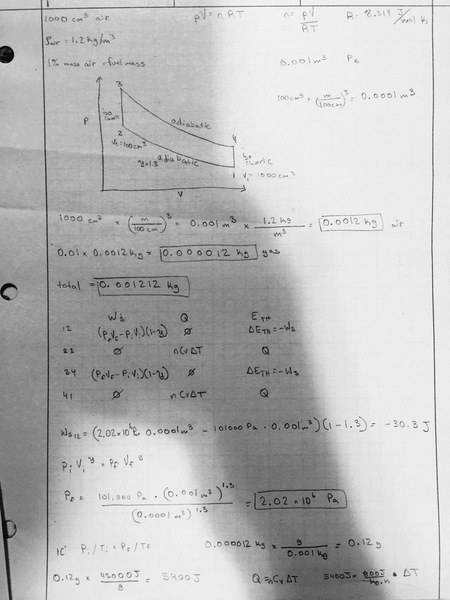

In a particular engine, a starts by taking in 1000cm3 of air (p=1.2kg/m3). Next, an amount of fuel is added equivalent to 1% of the mass of the air in the piston (since gasoline is composed of large molecules, assume that this does not affect the pressure in the piston). The piston is then compressed to a volume of 100cm3. This compression can be assumed to be adiabatic with PV1.3 being constant. Next, the fuel is ignited, releasing an energy of 45000J for every gram of fuel in the form of heat, while the piston stays at constant volume. You may assume that the heat capacity at constant volume for this gas is 800J/kg*K. After combustion, the piston expands back to the original volume of 1000cm3 adiabatically, and the gasses are released.
1) What is the work required to compress the gas during compression, work done by the gas during the expansion, and total work done during the cycle.?
2) How much heat is added to the system during the combustion stage?
Hint: You may want to answer questions 1&2 together in the form of a U table
3) What is the efficiency of this particular cycle?
4) What is the temperature of the released gas?
Equations we have learned in this section...
PV=NKBT
W=PV
E=Q - W
E=CvT
Was told to utilize google for any other equations or constants that may be useful...
This is how I started working stuff out... but have no idea what I'm actually doing.