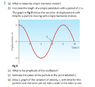
How is the Answer to 3(d) Found in Simple Harmonic Motion Problem?
- Thread starter tahmidbro
- Start date
Click For Summary
SUMMARY
The discussion centers on calculating the velocity in a simple harmonic motion problem, specifically addressing the discrepancy between a calculated velocity of 0.0235 m/s and an answer key value of 6 m/s. The user utilized the derivative of the cosine function and the formula v = -Aw sin(wt) to derive the velocity, where the amplitude (A) is 3 cm and the period is 8 seconds. The calculated angular frequency (w) is 0.785 rad/s, leading to confusion regarding the accuracy of the provided answer key.
PREREQUISITES- Understanding of simple harmonic motion principles
- Knowledge of derivatives in calculus
- Familiarity with the formula v = -Aw sin(wt)
- Ability to calculate angular frequency (w) from the period
- Review the derivation of velocity in simple harmonic motion using calculus
- Learn about the relationship between amplitude, period, and maximum velocity
- Investigate common errors in simple harmonic motion problem-solving
- Explore additional resources on simple harmonic motion equations and their applications
Students studying physics, particularly those focusing on mechanics and simple harmonic motion, as well as educators seeking clarification on common calculation errors in this topic.
Similar threads
- · Replies 1 ·
- · Replies 51 ·
- · Replies 5 ·
- · Replies 13 ·
- · Replies 11 ·
- · Replies 2 ·
- · Replies 17 ·