AlephClo
- 32
- 1
The Coriolis potential last term of (42) is obtained by integration through r and R from last term of (40).
I do not understand why we do not need to integrate through v as well, since the Coriolis force depends on v?
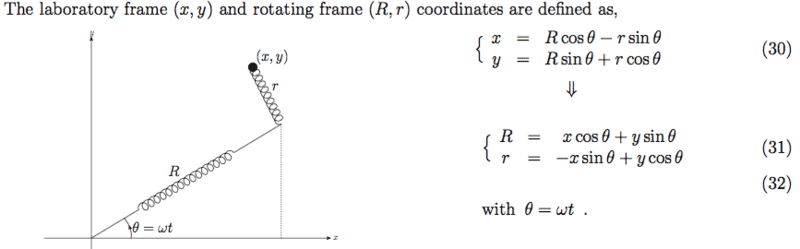

Equation (41) is wrong I think, L must be replaced by U.
The forces for the 2 springs are F(r)= -kr, and F(R)= -kR (bold are vectors)
The generalized force Qj = Fi ⋅ δri/δqj (δ is del the partial derivative; j and i are indices)
the 4 terms of (42) are obtainable from the intergration relatively to r and R.
Since the Coriolis force is dependent of the velocity v, why we do not need to Integration relative to v = (dr/dt, dR/dt) as well?
Or more generally when is it required that we integrate through position and velocity the force that depends on position and velocity to obtain a generalized potential.
Thank you.
I do not understand why we do not need to integrate through v as well, since the Coriolis force depends on v?
Homework Equations
Equation (41) is wrong I think, L must be replaced by U.
The forces for the 2 springs are F(r)= -kr, and F(R)= -kR (bold are vectors)
The generalized force Qj = Fi ⋅ δri/δqj (δ is del the partial derivative; j and i are indices)
The Attempt at a Solution
the 4 terms of (42) are obtainable from the intergration relatively to r and R.
Since the Coriolis force is dependent of the velocity v, why we do not need to Integration relative to v = (dr/dt, dR/dt) as well?
Or more generally when is it required that we integrate through position and velocity the force that depends on position and velocity to obtain a generalized potential.
Thank you.
