How is the Horizon Drop Calculated Due to Earth's Curvature?

[Axion]

I propose a calculation of the drop X in the horizon that an observer sees due to the curvature of the Earth surface the parameters are:

h: the elevation of the observer from the surface of the Earth in km
H: the length of the horizon at which the drop is perceived in km
R: the radius of the spherical Earth ≈ 6371 km
d: the distance from the observer to the horizon in km

The following ( see figure 1) sets the layout for the calculation, the observer field of view intersects the globe in the circle (C).

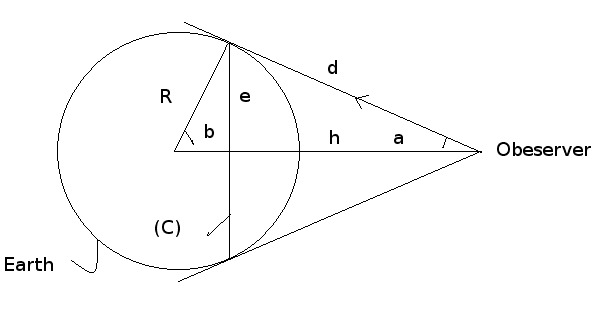
Computing d:
We have: (R+h)²=d²+R²

⇒ d=√(2hR+h²)

Computing e: e is the radius of (C)

we have sin(b)=cos(a)⇒ e/R=√(1-(e/d)²)⇒e=Rd/√(R²+d²)

Now switching to the plane of the circle (C) (see figure 2):

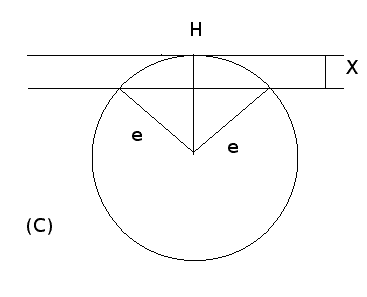
Computing the drop X(h,H):

X=e-√(e²-H²/4)

Now under the reasonable approximation that h<<R:

X(h, H)=H²/2√(Rh)⇒ X(h, H)=0.00626×H²/√h (km)

For example; if H=1 km and h=2 m (human height)⇒ X(1, 0.02)= 44.3 m .

 

[Drakkith]

Hi Axion! Welcome to PF!

That's an interesting calculation, but may I ask what the purpose of posting it here is? Just to share? Or did you have a question about it?

 

[Axion]

Hi Axion! Welcome to PF!

That's an interesting calculation, but may I ask what the purpose of posting it here is? Just to share? Or did you have a question about it?

Hi,
Just to share may be someone will need it.