How is the Sine law written for this problem?

[Benjamin_harsh]

Homework Statement

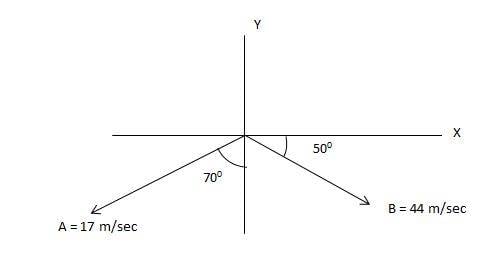
Find the resultant vector of vectors A and B shown in the figure.

Relevant Equations

$\large \frac {R}{Sin 70^0} = \frac {17}{Sin\alpha}$

Find the resultant vector of vectors A and B shown in the figure.

Solution:
By geometry method:

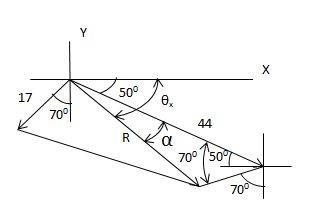
Cosine law for the right side triangle.

$R^{2} = 17^{2} + 44^{2} - 2 (17)(14).cos 70^{0}$

$R = 41.39 m/sec$

By Sin law,

$\large\frac {R}{Sin 70^0} = \frac {17}{Sin\alpha}$

$sin \alpha = \large \frac{17.sin 70^{0}}{R} = \frac{17.sin 70^{0}}{41.39}$

$\alpha = 22.70^{0}$

$\theta_{x} = 50 + \alpha = 50 + 22.70$

$\theta_{x} = 72.70^{0}$

 

[BvU]

Is there a question here ?

PS tip: in $\LaTeX$, use \sin and not Sin or sin
Idem \cos, \tan, \log, etc.

 

[SammyS]

By Sin law,

$\large\frac {R}{Sin 70^0} = \frac {17}{Sin\alpha}$

$sin \alpha = \large \frac{17.sin 70^{0}}{R} = \frac{17.sin 70^{0}}{41.39}$

Expanding a bit on @BvU's comments regarding $\LaTeX :$

Your code for the expression:
$\large\frac {R}{Sin 70^0} = \frac {17}{Sin\alpha}$

is: ##\large\frac {R}{Sin 70^0} = \frac {17}{Sin\alpha}##.

As BvU recommends, use "\sin" rather than "Sin".
Also, there is no degree symbol built into $\LaTeX$. Using "^0", as you did, is one work-around. Another is to use "^\circ".
You can get large fractions by using "\dfrac" rather than "\large\frac". Using "\large" the way you did makes everything that follows large, not just the fraction. You could avoid making all that large by 'wrapping' the expression in braces: " { \large \frac{num}{denom} } ".

Using the following code: ##{\large\frac {R}{\sin 70^\circ}} = \dfrac {17}{\sin\alpha}## gives the result:

${\large\frac {R}{\sin 70^\circ}} = \dfrac {17}{\sin\alpha}$
(The first fraction is done using the "\large" feature)

One more thing:
Use "\cdot" rather than a period, ".", for multiplication.

##\sin \alpha = \dfrac{17 \cdot \sin 70 ^\circ }{R} = \dfrac{17 \cdot \sin 70^\circ }{41.39}## gives the result:

$\sin \alpha = \dfrac{17 \cdot \sin 70 ^\circ }{R} = \dfrac{17 \cdot \sin 70^\circ }{41.39}$

 

[Benjamin_harsh]

I am not asking about LATEX. I am asking about concept.

 

[SammyS]

I am not asking about LATEX. I am asking about concept.

Yup. Looks good.

So your resultant vector has a magnitude of 41.39 m/s and makes an angle of $72.70^\circ$ clockwise from the positive $x$-axis.​

You can check your answer using x-components and y-components.

The $\LaTeX$ tips were given free of charge by @BvU and me.

 

[Benjamin_harsh]

Please explain this sin law equation. $\large \frac {R}{sin70_{0}} = \frac{17}{sin \alpha}$.?
$70^{0}$ is not the full angle, It is just a portion of the angle. So how sine law is calculated on portion of the angle?

 

[BvU]

It's the full angle: the 70$^\circ$ is shown in the right half of the figure (that you should redraw a bit more to scale).

 

[Benjamin_harsh]

How $17$ included in the sine law? See, in the diagram, $17$ is far away from $\alpha$ so how it is included ?

 

[BvU]

Did you already re-draw the picture a bit more to scale as I suggested ?
Then you'll see more easily where the 17 is sitting: opposite the angle $\alpha$.
Please do a little bit of pondering answers before shooting off yet another question

 

[SammyS]

@Benjamin_harsh ,
Here is your figure redone to scale.

 

[BvU]

Demonstrating a mstery of which drawing program, exactly ?

 

[SammyS]

Demonstrating a mastery of which drawing program, exactly ?

I used LibreOffice Draw.

To call my abilities to use it "mastery" would be a stretch. I almost gave up using it (for making this figure) but then made a small break-through with making circular arcs. I can now make the arc I want in about half of my attempts.

 

[neilparker62]

Please explain this sin law equation. $\large \frac {R}{sin70_{0}} = \frac{17}{sin \alpha}$.?
$70^{0}$ is not the full angle, It is just a portion of the angle. So how sine law is calculated on portion of the angle?

For the record, it's also possible to calculate $\alpha$ without recourse to R or the sin rule. Referring to SammyS's very excellent diagram, drop a perpendicular from where the green arrows meet to the side of length 44. Then: $$ \tan{\alpha} = \frac{17\sin{70^\circ}}{44-17\cos{70^\circ}} $$ This is the 'tan rule' but unfortunately nobody ever teaches it in school!

PS: have picked up all the above 'tips' re use of $\LaTeX$!