JasonR2
- 2
- 0
Homework Statement
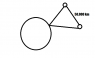
Question: If a broadcast of a sporting event went up to a geostationary satellite, then traveled 50 000 km to another geostationary satellite, then came back to earth, what would be the delay in the signal? All electromagnetic waves travel at the speed of light, and most of the route would be in a vacuum. Also, remember that the path starts and ends at at the Earth's surface, not at the center of the Earth.
Variables:
c = 299 792 458 m / s
distance between two satellites = 50,000 km or 5.0 x 10^7 m
Other variables:
G = 6.674 x 10 ^ -11 m ^3 / kg/
Me (mass of earth) = 5.97219 x 10^ 24 kg
sd (Seconds in a day) = 86400 seconds
Homework Equations
L= 2 * pi *rL = V/T
V = sqrt(G * Me / r)
From those the equation below is derived...
r = ((sd * sqrt(G * Me)) / (2 * pi) )^ (2/3)
v = d/t
The Attempt at a Solution
I found that the geostationary radius (r_) is 4.22 x 10^ 7 m or 4.22 x 10^4 km. Which is confirmed is confirmed correct.
My problem is I don't know where to go from here I'm assuming I have to use the geostationary radius (r_) calculated and the speed of light (c). So the formula V=D/T should be the one to use.
The answer is supposed to be 0.40 seconds
I thought that I might need to look for the hypotenuse so I tried the a^2 + b^2 = c^2 Using 4.22 x 10^7 as a and 5.0 x 10^7 as b. I end up getting 6.54 x 10 ^ 7 m. I then took that and plugged it into the V=D/T equation to solve for T. V = speed of light.
T = 6.54 x 10 ^ 7 / 3.0 x 10 ^ 8 = 0.218 seconds
Unfortunately I come out with 0.218 seconds not even close to the answer.
Where do I go from here? Thanks!