bradleyharmon
- 1
- 0
[Moderator note: Member advised to use the provided formatting template for all homework help requests]
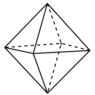
If each side of a tetrahedron is an equilateral triangle painted white or black, five distinct patterns are possible: all sides white, all black, just one side white, just one black, and two sides white and two black. If each side of an octahedron is a white or black equilateral triangle, how many distinct patterns are possible?
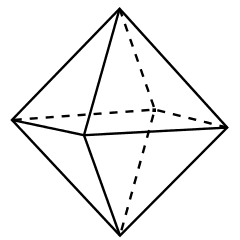
My own approach to this problem was simply to add a new triangle of one set color and build up until I reached 4 black and 4 white since 5 white or 5 black would imply 3 black and 3 white, respectively, and so on for 6/2. So, there's only one way to make it all white or all black. And there seems to also be only one way to make it 1 black and 7 white and 1 way to make it 7 white and 1 black. Counting all of the way up, I have just over 20 total ways. Does anyone have a different approach to this problem or an equation that could simplify it?
If each side of a tetrahedron is an equilateral triangle painted white or black, five distinct patterns are possible: all sides white, all black, just one side white, just one black, and two sides white and two black. If each side of an octahedron is a white or black equilateral triangle, how many distinct patterns are possible?
My own approach to this problem was simply to add a new triangle of one set color and build up until I reached 4 black and 4 white since 5 white or 5 black would imply 3 black and 3 white, respectively, and so on for 6/2. So, there's only one way to make it all white or all black. And there seems to also be only one way to make it 1 black and 7 white and 1 way to make it 7 white and 1 black. Counting all of the way up, I have just over 20 total ways. Does anyone have a different approach to this problem or an equation that could simplify it?
Attachments
Last edited by a moderator: