How much KE does the system start with?

[Jared944]

Homework Statement

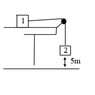
Two boxes are set up in a system as shown in the attached picture.

Box 1 - mass = 5 kg
Box 2 - mass = 2 kg

h = 5m

The system is released, and box 2 hits the ground. With a frictionless system, find the total KE before box 2 hits the ground.

Homework Equations

I am fairly sure I have to use the conservation of energy, which in this case would be:

(1/2)*m*vf^2=m*g*h

((1/2)*m*vf^2)-(m*g*h)=KE

The Attempt at a Solution

I don't quite understand how to go about this problem with the two box system. I can figure out the boxes force and acceleration, but not what I need.

Thanks,

 

[radou]

Unfortunately, the attachment doesn't seem to be approved yet. What exactly does 'h' represent?

 

[Jared944]

Oh, ok.

Block 1 is sitting on a (frictionless) table attached to block 2 which is hanging off of the table. Both blocks are attached by a rope and a (frictionless) pully.

Before the system is released, block 2 is 5m from the ground (h = 5m)

Thanks for the obervation about the pic...

 

[radou]

You were right when you said you have to use energy conservation. Since the block are connected with a rope, and since there is no friction, in what relation are the velocities of the blocks?

 

[Jared944]

The velocities should be the same. However, I've calculated the acceleration and the Tension of the blocks in motion. The acceleration and T of block 2 can be illustrated as T-w2=m2(-a)
And Block 1 can be illustrated as 0+T=m1*a

The tension turnes out to be 14 N and the acceleration is 2.8 m/s^2

Im not sure how to use the data...

 

[radou]

The velocities should be the same. However, I've calculated the acceleration and the Tension of the blocks in motion. The acceleration and T of block 2 can be illustrated as T-w2=m2(-a)
And Block 1 can be illustrated as 0+T=m1*a

The tension turnes out to be 7.35 N and the acceleration is 2.45 m/s^2

Im not sure how to use the data...

Do you need the acceleration and the tension? Think about how the kinetic energy of the system is defined.

 

[Jared944]

So, KE = mgh + w
KE = 2*-9.8*5+14
KE = -84J? How can I reach a negative KE?

 

[radou]

So, KE = mgh + w
KE = 2*-9.8*5+14
KE = -84J? How can I reach a negative KE?

What exactly is w?

Do you agree if we say that the total kinetic energy of the system equals 1/2 M v^2 + 1/2 m v^2 ?

 

[Jared944]

of course... I was thinking w was the work done by the tension of the system.

 

[Doc Al]

of course... I was thinking w was the work done by the tension of the system.

The tension is an internal force and does no net work on the system as a whole. If you were to analyze one mass by itself, then you would need to include the work done by the tension force.

Note also: When calculating changes in gravitational PE using mg\Delta h, g is just a positive number (g = 9.8 m/s^2, not -9.8 m/s^2). g is just the magnitude of the acceleration due to gravity.