Jaydude
- 3
- 0
1. The problem statement:
A removable plate is mounted in the end of a swimming pool. The plate is 60cm square with the top edge 30cm below surface of water. Compute the force on plate and distance to centre of pressure below surface of water.
2. Homework Equations .
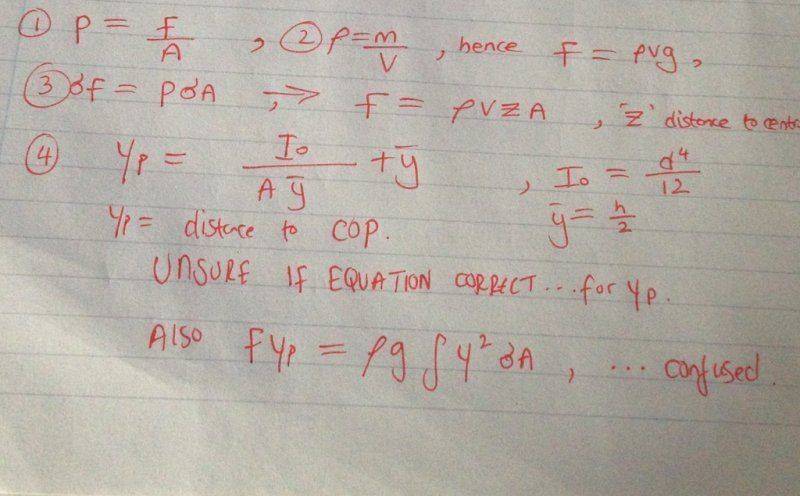
3. The attempt at solution :
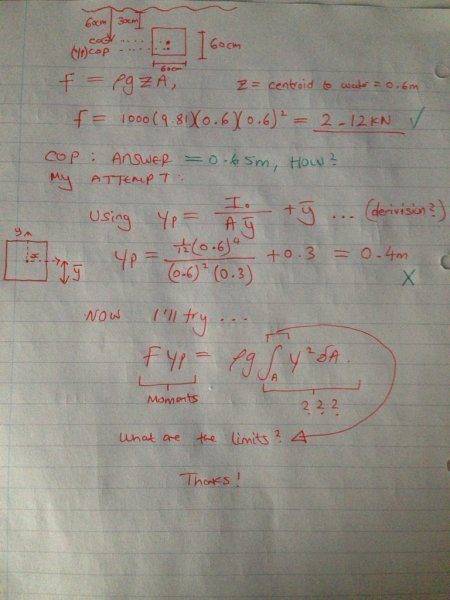
Spent a lot of research and time on cop to no avail, so this is my last resort!
Kind regards ,
Jay
A removable plate is mounted in the end of a swimming pool. The plate is 60cm square with the top edge 30cm below surface of water. Compute the force on plate and distance to centre of pressure below surface of water.
2. Homework Equations .
3. The attempt at solution :
Spent a lot of research and time on cop to no avail, so this is my last resort!
Kind regards ,
Jay