adamaero
- 109
- 1
- Homework Statement
- How to calculate rotor flux of the three phase squirrel cage induction motor?
- Relevant Equations
- Rotor flux and more
Three phase squirrel cage induction motor with given parameters (stator winding connected in delta)
I have been struggling with calculation of the nominal value of the rotor flux. My idea was that I will use the T equivalent circuit for that purpose
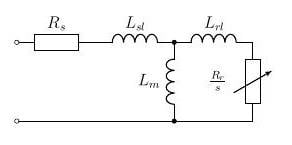
and I will use nominal values of the motor quantities i.e. I set the motor operating point into the nominal operation point (nominal slip, nominal stator voltage etc.). Then I calculate phasor of the stator current (Is) and phasor of the rotor current (Ir) according to the below given set of equations
https://forum.allaboutcircuits.com/attachments/1620849888346-png.238168/
For the motor parameters mentioned above the Scilab command linsolve gave mehttps://forum.allaboutcircuits.com/attachments/1620849901203-png.238169/
Based on the known phasors of the stator and rotor current I used the below given equation for calculation of the phasor of the rotor flux
https://forum.allaboutcircuits.com/attachments/1620849925020-png.238170/
which gives λr=0.5554856−0.0613638j i.e. |λr|=0.5588647V⋅s.
This value seems to me to be too low. So I have doubts regarding the way I have used for its calculation. Unfortunately I don't know any other way for its calculation which I can use for verification. Can anybody tell me whether the applied procedure is correct or not?
- nominal power: Pn=22.4kW
- nominal stator voltage: Vsn=230V
- nominal stator current: Isn=39.5A
- nominal stator frequency: fsn=60Hz
- nominal speed: nn=1168min−1
- number of pole pairs: 3
- stator resistance per phase (T equivalent circuit): Rs=0.294Ω
- stator leakage inductance per phase (T equivalent circuit): Lsl=0.00139H
- rotor resistance per phase (T equivalent circuit): Rr=0.156Ω
- rotor leakage inductance per phase (T equivalent circuit): Lrl=0.0007401H
- magnetizing inductance per phase (T equivalent circuit): Lm=0.041H
I have been struggling with calculation of the nominal value of the rotor flux. My idea was that I will use the T equivalent circuit for that purpose
and I will use nominal values of the motor quantities i.e. I set the motor operating point into the nominal operation point (nominal slip, nominal stator voltage etc.). Then I calculate phasor of the stator current (Is) and phasor of the rotor current (Ir) according to the below given set of equations
https://forum.allaboutcircuits.com/attachments/1620849888346-png.238168/
For the motor parameters mentioned above the Scilab command linsolve gave mehttps://forum.allaboutcircuits.com/attachments/1620849901203-png.238169/
Based on the known phasors of the stator and rotor current I used the below given equation for calculation of the phasor of the rotor flux
https://forum.allaboutcircuits.com/attachments/1620849925020-png.238170/
which gives λr=0.5554856−0.0613638j i.e. |λr|=0.5588647V⋅s.
This value seems to me to be too low. So I have doubts regarding the way I have used for its calculation. Unfortunately I don't know any other way for its calculation which I can use for verification. Can anybody tell me whether the applied procedure is correct or not?