How to calculate velocities/forces from sphere collisions?

[cvex]

Hi,

Basically I have a point cloud that represents balls with different radii. They are all moving based on forces and sometimes they are intersecting with each other.

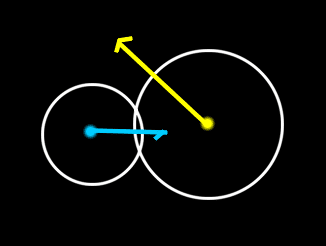
Imagine the yellow ball is going in one direction while the blue balls goes in another direction. At one time they are colliding. How can I affect each sphere,s velocity or force so I can update it after the collision?

What I know are these:

1. Since everything is represented as points, I know the position of the point that intersects with me given each of their radii.

2. I know the distance between them.

3. I know their velocity.

4. I know what forces are acting on these but they are integrated onto velocity at each iteration.

5. I know their radii.

6. I know their mass but it can be ignored.

7. I know their surface friction but this can also be ignored.If it was a simple repulsion, I would just negate the velocity but it will depend on where on the sphere the other sphere hits, right? That's where I have no idea how to solve this.

Any ideas?Thanks a lot.

 

[BiGyElLoWhAt]

Can you set up a system of equations using the velocities and radii of the circles to find the collision points? Then perhaps apply conservation of momentum to find the final velocities of the system's?

 

[cvex]

Thanks I can. This is inside a 3d app. So what you do is add nodes to modify the behaviour of particles. They generally modify force and the particle solver integrates it onto velocity.

So if I can calculate what kind of force is produced from the collisions, I can easily do it. I just don't know how to set it up with spheres and the point of impact.

Normally they have a rigid body solver that can do this easily. I just wanted to do it with particles for fun.

 

[BiGyElLoWhAt]

You mean the resultant force? Well it would be normal to the contact tangent. So if you can figure out the point of conract, you'll have a point there (im assuming 3 coords?) The difference in coords will be the opposite the direction of the force on that sphere.

 

[cvex]

Thanks a lot. Since these are all particles, I don't have the point of contact, just that some point with a radius A is within my radius of B and so I should react. I need to find a way to find this point of contact given the 2 centers of the spheres and radii. Can that be done mathematically?

 

[BiGyElLoWhAt]

Oh ill giarantee it can, the question is how... how are you tracking the spheres? Do you track them as a whole or do you just track the center and know where the shell is?

 

[cvex]

I am just tracking the centers and know their radii. I made more progress though. I just need to perform moving sphere sphere collision like this:

"Moving Sphere/Sphere: (location) Add the radius of the moving sphere to the static sphere, and treat the moving sphere as a ray. Use this ray to perform ray/sphere intersection. See Gomez; Schroeder for code (article has bug in derivation, code is fine); and RTR2, p. 622."

If I do this, I should have hitpoint, normal, distance, etc so after that only thing I would need is to figure out how to calculate a force from that so I can apply it to the current point/sphere.

 

[BiGyElLoWhAt]

So this is just between 2 spheres and they have 1 collision?
The force is going to depend on the object you want them to model. Maybe you should treat them as having a membrane? Then model the interaction as a spring, with x being the radius and x hat (direction) being in the radial direction (which we talked about earlier). Or are you looking for more of a pool ball interaction? Try giving this a look. They seem to do a decent job explaining it: http://www.real-world-physics-problems.com/physics-of-billiards.html

 

[BiGyElLoWhAt]

The only thing I'm going to say about what you posted, is that it works for 2 spheres, but gets sufficiently more complex for multiple spheres of different sizes, if it even works at all. If it's a larger sample, you'll want to do that but with an if statement that checks during every step of motion in your while loop. Then call the calculation function, and use that to determine your force.

 

[BiGyElLoWhAt]

Actually, here's someone using hooke's law for billiards as well: http://archive.ncsa.illinois.edu/Classes/MATH198/townsend/math.html

 

[cvex]

Thanks the first link doesn't work but I want a billiard kind of interactions between the balls.

 

[BiGyElLoWhAt]

The second link goes through and gives some good insight on how to make this happen with springs. They say basically (loose paraphrasing) 'Billiards are really stiff springs, this is how you model a spring'.
So they solve for your change in velocity, which is ultimately what you're looking for, right? The only thing, is that you'll have to break this down into chunks, or pixelate it, or step it or however you want to call it. So the premise is this: billiards are springs. The spring constant is fixed, and the mass of the oscillator (the mass of the billiard ball) is fixed, therefore the time it takes for the collision to occur is fixed. If you've studied lagrangian mechanics/oscillators (these 2 seem to go hand in hand), you'll have seen $\omega = \sqrt{\frac{k}{m}}$ with omega being angular velocity, or rate of compression of the spring (billiard ball), k being the spring constant, and m being the mass.

So go through the article, or at least the first little bit, as that's what I thought was necessary, decide on the mass of the objects, the spring constant, and that will give you the time you need. Then, along with the angle of the collision (arctangent function in code), you can get the direction of the force. Now you have the magnitude of the the force, the time interval for the force, and the direction for the force: everything you need for a vector impulse, which is the change in momentum, and change in momentum/mass is change in velocity.