zenterix
- 774
- 84
- Homework Statement
- I have a question regarding a mathematical tool used a lot in physics apparently: Taylor expansions.
- Relevant Equations
- Here is the context.
I calculated the electric field at a particular point in 3D space.
$$E_p=\begin{cases}
\frac{2k_eQ}{R^2}(1-\frac{z}{(z^2+R^2)^{1/2}}) & \text{for } z \geq 0\\
\frac{2k_eQ}{R^2}(-1-\frac{z}{(z^2+R^2)^{1/2}}) & \text{for } z < 0\\
\end{cases}$$
And I am interested in knowing what happens when ##z>>R##
First, to isolate just the mathematical operation of Taylor expansion, let's consider
$$\frac{z}{(z^2+R^2)^{1/2}}$$
$$=\frac{1}{(1+\frac{R^2}{z^2})^{1/2}}$$
When ##z>>R## we also have ##\frac{R}{z}## and ##\frac{R^2}{z^2}## both approach zero.
Consider two different Taylor expansions.
First, let ##f_1(s)=(1+s)^{1/2}##
$$f_1'(s)=-\frac{1}{2(1+s^{3/2})}$$
Near ##s=0##, we have the first order Taylor expansion
$$f_1(s) \approx 1 - \frac{s}{2}$$
Now consider a different choice for ##f(s)##
$$f_2(s)=(1+s^2)^{1/2}$$
$$f_2'(s)=-\frac{s}{(1+s)^{3/2}}$$
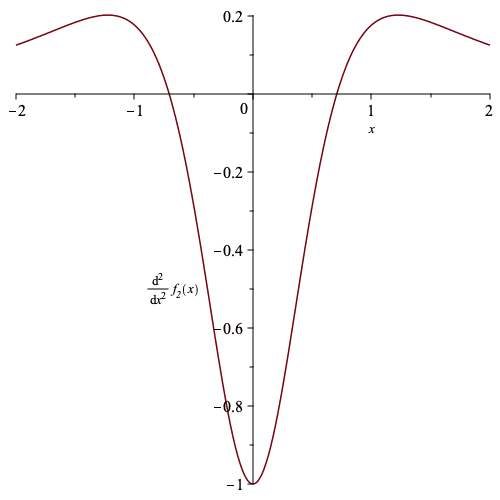
$$f_2''(s)=-\frac{1}{(1+s)^{1/2}}+\frac{3s^2}{(1+s^2)^{5/2}}$$
Near ##s=0##, we have the first order Taylor expansion
$$f_2(s)\approx 1$$
and the second order Taylor expansion
$$f_2(s) \approx 1 - \frac{s^2}{2}$$
My question is simply: how do we choose which approximation to use?
Considering the original context of what happens to the electric field if ##z>>R##, it appears that the choice of Taylor expansion doesn't affect the result. I guess I am trying to wrap my head around the intuition of why this is.
If I use ##f_1##, then
$$E_p=\begin{cases}
\frac{2k_eQ}{R^2}(1-1+\frac{R^2}{2z^2}) & \text{for } z \geq 0\\
\frac{2k_eQ}{R^2}(-1-1+\frac{R^2}{2z^2}) & \text{for } z < 0\\
\end{cases}$$
$$E_p=\begin{cases}
\frac{k_eQ}{z^2} & \text{for } z \geq 0\\
\frac{k_eQ}{z^2}-\frac{4k_eQ}{R^2} & \text{for } z < 0\\
\end{cases}$$
If I use ##f_2##, then
$$E_p=\begin{cases}
\frac{2K_eQ}{R^2}(1-1+\frac{R^4}{2z^4}) & \text{for } z \geq 0\\
\frac{2K_eQ}{R^2}(-1-1+\frac{R^4}{2z^4}) & \text{for } z < 0\\
\end{cases}$$
$$E_p=\begin{cases}
\frac{k_eQ}{z^2} & \text{for } z \geq 0\\
\frac{k_eQ}{z^2}-\frac{4k_eQ}{R^2} & \text{for } z < 0\\
\end{cases}$$
ie, same result in both cases.Here are some plots
First, let ##f_1(s)=(1+s)^{1/2}##
$$f_1'(s)=-\frac{1}{2(1+s^{3/2})}$$
Near ##s=0##, we have the first order Taylor expansion
$$f_1(s) \approx 1 - \frac{s}{2}$$
Now consider a different choice for ##f(s)##
$$f_2(s)=(1+s^2)^{1/2}$$
$$f_2'(s)=-\frac{s}{(1+s)^{3/2}}$$
$$f_2''(s)=-\frac{1}{(1+s)^{1/2}}+\frac{3s^2}{(1+s^2)^{5/2}}$$
Near ##s=0##, we have the first order Taylor expansion
$$f_2(s)\approx 1$$
and the second order Taylor expansion
$$f_2(s) \approx 1 - \frac{s^2}{2}$$
My question is simply: how do we choose which approximation to use?
Considering the original context of what happens to the electric field if ##z>>R##, it appears that the choice of Taylor expansion doesn't affect the result. I guess I am trying to wrap my head around the intuition of why this is.
If I use ##f_1##, then
$$E_p=\begin{cases}
\frac{2k_eQ}{R^2}(1-1+\frac{R^2}{2z^2}) & \text{for } z \geq 0\\
\frac{2k_eQ}{R^2}(-1-1+\frac{R^2}{2z^2}) & \text{for } z < 0\\
\end{cases}$$
$$E_p=\begin{cases}
\frac{k_eQ}{z^2} & \text{for } z \geq 0\\
\frac{k_eQ}{z^2}-\frac{4k_eQ}{R^2} & \text{for } z < 0\\
\end{cases}$$
If I use ##f_2##, then
$$E_p=\begin{cases}
\frac{2K_eQ}{R^2}(1-1+\frac{R^4}{2z^4}) & \text{for } z \geq 0\\
\frac{2K_eQ}{R^2}(-1-1+\frac{R^4}{2z^4}) & \text{for } z < 0\\
\end{cases}$$
$$E_p=\begin{cases}
\frac{k_eQ}{z^2} & \text{for } z \geq 0\\
\frac{k_eQ}{z^2}-\frac{4k_eQ}{R^2} & \text{for } z < 0\\
\end{cases}$$
ie, same result in both cases.Here are some plots
Last edited: