Conducting rod in equilibrium due to magnetic force

[lorenz0]

Homework Statement

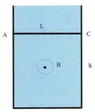
A conducting rod $AC$ of mass $m=0.1\ kg$, length $L=1\ m$ and resistance $R=5\ \Omega$ can move without friction on two metallic rails in a region where there is a uniform magnetic field, perpendicular to the plane of the circuit and with magnitude changing with time.
$B(t_0=0)=2\ T$ and the rod is in equilibrium at height $h=3\ m$.

(a) Determine the magnetic force, the current (in direction and magnitude) and the electromotive force induced at time $t_0=0$.
(b) Verify that if $B(t)=B_0\sqrt{1-At}$ the magnetic force is constant and find the value of $A$ such that the rod remains still.
(c) In these conditions, find the total charge that has gone around the circuit in the time interval from $t_0=0\ s$ to $t_1=10\ s$.
(d) Find out for how much time the rod remains in equilibrium.

Relevant Equations

$F_{m}=I\vec{L}\times\vec{B},\ \mathcal{E}=-\frac{d\phi(\vec{B})}{dt},\ V=IR$

I am having problems understanding point (b) so I would like to know if my reasoning in that part is correct and/or how to think about that part because I don't see how to justify the assumption $v_y=0\ m/s$. Thanks.

I set up the $xyz$ coordinates system in the usual way with $xy$ in the plane and $z$ pointing upwards.

(a) The current at time $0$, $i(0)$ should go around in a counterclockwise fashion otherwise it would help the weight pull the rod down and also $i(0)LB(0)=mg\Rightarrow i(0)=\frac{mg}{LB(0)}$ (1).
Also, by Ohm's Law we have that the electromotive force is $\mathcal{E(0)}=i(0)R\overset{(1)}{=}\frac{mg}{LB(0)}$.

(b)
$i(t)=\frac{\mathcal{E(t)}}{R}=\frac{1}{R}(-\frac{d\phi(\vec{B})}{dt})=-\frac{1}{R}(\frac{d}{dt}\int_{S}\vec{B}\cdot d\vec{S})=-\frac{1}{R}(\frac{d}{dt}\int_{S}B_0\sqrt{1-At}dS)=-\frac{B_0}{R}(\frac{d}{dt}\sqrt{1-At}\int_S dS)=-\frac{B_0}{R}(\frac{d}{dt}\sqrt{1-At}\int_{0}^{y} L d\bar{y})=-\frac{LB_0}{R}(\frac{d}{dt}\sqrt{1-At} y)=-\frac{LB_0}{R}\left( -\frac{A}{2\sqrt{1-At}}\cdot y+\sqrt{1-At}\cdot v_y \right)$

so

$F_m(t)=i(t)LB(t)=-\frac{LB_0}{R}\left( -\frac{A}{2\sqrt{1-At}}\cdot y+\sqrt{1-At}\cdot v_y \right)\cdot L\cdot B_0\sqrt{1-At}=-\frac{L^2B_0^2}{R}\left( -\frac{A}{2}y+(1-At)v_y \right)$

so it seems to me that the only way that the magnetic force could be constant is if $v_y=0$ but can I assume this?

In that case $F_m=\frac{L^2B_0^2 A}{2R}y$ and to balance the weight it should be $F_m-mg=0\Leftrightarrow \frac{L^2B_0^2 A}{2R}y=mg\Leftrightarrow A=\frac{2Rmg}{yL^2B_0^2}$ but I am not sure which $y$ I should pick.

(c) $q=\int_{t=0\ s}^{t=10\ s}i(t) dt$

 

[kuruman]

I don't think you have been careful enough with part (a). If the at t = 0 the rod is in equilibrium, that means it is not moving. You have the weight $mg$ down and the magnetic force $F_M$ up and the two must be equal. Consider that $$\frac{d\Phi}{dt}=\frac{d}{dt}(BA)=B\frac{dA}{dt}+A\frac{dB}{dt}.$$This allows you to find the time derivative of the magnetic field at $t_0$. I would write a differential equation for Newton's second law.

 

[lorenz0]

I don't think you have been careful enough with part (a). If the at t = 0 the rod is in equilibrium, that means it is not moving. You have the weight $mg$ down and the magnetic force $F_M$ up and the two must be equal. Consider that $$\frac{d\Phi}{dt}=\frac{d}{dt}(BA)=B\frac{dA}{dt}+A\frac{dB}{dt}.$$This allows you to find the time derivative of the magnetic field at $t_0$. I would write a differential equation for Newton's second law.

I don't completely get what you are suggesting but I tried and got: $iR=-\frac{d\Phi}{dt}=BL\frac{dy}{dt}+Ly\frac{dB}{dt}=Ly\frac{dB}{dt}$ and substituting in Newton's second law I would get: $$iLB-mg=0\Rightarrow -\frac{L^2yB}{R}\frac{dB}{dt}-mg=0\Rightarrow \frac{L^2 hB}{R}\frac{dB(0)}{dt}=-mg\Rightarrow \frac{dB(0)}{dt}=-\frac{mgR}{L^2hB(0)}$$ but I don't see how knowing $\frac{dB(0)}{dt}$ helps me (and also what is wrong with the way I found $i(0)$ out originally)

 

[kuruman]

First, in part (a) you are asked to find the magnetic force. That means an expression for the magnetic force in terms of the variables. To do this correctly, you need to find a general expression and then see what happens at $t_0=0$. You have at any time a current magnitude $$i(t)=\frac{1}{R}\left(B\frac{dA}{dt}+A\frac{dB}{dt}\right)=\frac{1}{R}\left(BL\frac{dy}{dt}+Ly\frac{dB}{dt}\right).$$At time $t_0=0$ you need to be careful with the derivatives.

$$i(0)=\frac{1}{R}\left(B(0)L\left. \frac{dy}{dt}\right |_{t=0}+Ly(0)\left.\frac{dB}{dt}\right|_{t=0}\right).$$You multiply that by $LB(0)$ to get the magnitude of the magnetic force.

 

[Charles Link]

One comment is that they could have picked a better letter for the time dependence of the magnetic field. The letter "A" is needed for area, and the letter "a" for acceleration. The letter "b" would work better, for less confusion, i.e. $B(t)=B_o \sqrt{1-bt}$.
In any case, the statement of the problem wasn't completely clear, but I do think we are supposed to include gravity acting in the downward direction.

 

[kuruman]

In any case, the statement of the problem wasn't completely clear, but I do think we are supposed to include gravity acting in the downward direction.

Yes, the rod would not be in equilibrium if $F_M$ is the only force acting on it.

 

[Charles Link]

For part (b), perhaps I need to double-check my calculation, but I don't know that I agree with their claim that the magnetic force is constant, i.e. independent of time for the given $B(t)$. I have an expression for the force that contains $y(t)$ and $v_y(t)$. If the force is constant, then $y(t)=y_o+\frac{at^2}{2}$, and $v_y(t)=at$. When these are substituted back into the expression for the force, it seems there is a time dependence. Perhaps I made an error somewhere...

Edit: Reading the problem more carefully, I see they give initial conditions that essentially mean that $a=0$, and with that part included, yes the magnetic force is constant...

 

[kuruman]

Yes, the force is constant.

 

[Delta2]

on a side note, I think from Maxwell's equations it follows that we can't have as solution a magnetic field that is spatially homogeneous and time varying according to the given function for $B(t)$.

 

[Charles Link]

on a side note, I think from Maxwell's equations it follows that we can't have as solution a magnetic field that is spatially homogeneous and time varying according to the given function for $B(t)$.

It would be possible to run a current through a solenoid with a specified waveform. The magnetic field is uniform inside the entire solenoid for a long solenoid. Meanwhile, I think the problem is somewhat lacking in the way they introduced the initial conditions. They could have treated the more general case first, and then have the reader solve for the constant that would make the acceleration zero. If my calculations are correct, the form of the time dependence of $B(t)$ does not make for zero acceleration, unless the constant in that formula is in fact a precise value.

 

[Delta2]

It would be possible to run a current through a solenoid with a specified waveform. The magnetic field is uniform inside the entire solenoid for a long solenoid.

By approximation yes we can have such B but not exact. My argument is as follows

From Faraday's law in differential form $$Curl(E)=-\frac{dB}{dt}\neq 0$$ hence it follows that E is spatially and temporally varying (if E was homogeneous then its curl would be zero).

Now from Ampere's law in differential form and in points in space where the current density is zero we ll have $$Curl (B)=-\mu_0\epsilon_0\frac{dE}{dt}$$ from which it follows that the curl of B depends on x,y,z,t, hence B depends on x,y,z,t too.

PS . The only thing I am not completely sure is that if E depends on x,y,z,t then dE/dt depends on x,y,z,t. It might be the case that taking the time derivative nullifies the dependence on x,y,z.

 

[lorenz0]

First, in part (a) you are asked to find the magnetic force. That means an expression for the magnetic force in terms of the variables. To do this correctly, you need to find a general expression and then see what happens at $t_0=0$. You have at any time a current magnitude $$i(t)=\frac{1}{R}\left(B\frac{dA}{dt}+A\frac{dB}{dt}\right)=\frac{1}{R}\left(BL\frac{dy}{dt}+Ly\frac{dB}{dt}\right).$$At time $t_0=0$ you need to be careful with the derivatives.

$$i(0)=\frac{1}{R}\left(B(0)L\left. \frac{dy}{dt}\right |_{t=0}+Ly(0)\left.\frac{dB}{dt}\right|_{t=0}\right).$$You multiply that by $LB(0)$ to get the magnitude of the magnetic force.

I get the same result I got in my initial answer: $i(0)=-\frac{Lh}{R}\frac{dB(0)}{dt}$, $i(0)LB(0)-mg=0\Rightarrow -\frac{L^2 hB(0)}{R}\frac{dB(0)}{dt}=mg\Rightarrow \frac{dB(0)}{dt}=-\frac{mgR}{L^2 hB(0)}$ so $i(0)=\frac{mg}{LB(0)}$

 

[lorenz0]

The problem is that with my $A=\frac{2Rmg}{hL^2B_0^2}$ I get a current $i(t)=-\frac{1}{R}\frac{d\phi(\vec{B})}{dt}=-\frac{1}{R}\frac{d}{dt}\int_{S}B_0\sqrt{1-\frac{2Rmg}{hL^2B_0^2}t}dS=-\frac{LhB_0}{R}\frac{d}{dt}\sqrt{1-\frac{2Rmg}{hL^2B_0^2}}=\frac{mg}{LB_0\sqrt{1-\frac{2Rmgt}{hL^2B_0^2}}}$ and since $\frac{2Rmgt}{hL^2B_0^2}=\frac{9.8}{12}$ I cannot integrate $i(t)$ in part (c) on the whole interval from $0$s to $10$s to find $i(t)$ because the argument of the square root because negative from a certain point onward in that interval.
I can't see what it is that I am misunderstanding.

 

[kuruman]

The problem is that with my $A=\frac{2Rmg}{hL^2B_0^2}$ I get a current $i(t)=-\frac{1}{R}\frac{d\phi(\vec{B})}{dt}=-\frac{1}{R}\frac{d}{dt}\int_{S}B_0\sqrt{1-\frac{2Rmg}{hL^2B_0^2}t}dt=-\frac{LhB_0}{R}\frac{d}{dt}\sqrt{1-\frac{2Rmg}{hL^2B_0^2}}=\frac{mg}{LB_0\sqrt{1-\frac{2Rmgt}{hL^2B_0^2}}}$ and since $\frac{2Rmgt}{hL^2B_0^2}=\frac{9.8}{12}$ I cannot integrate $i(t)$ in part (c) on the whole interval from $0$s to $10$s to find $i(t)$ because the argument of the square root because negative from a certain point onward in that interval.
I can't see what it is that I am misunderstanding.

You need to be more careful with what you put down. You wrote
$$i(t)=-\frac{1}{R}\frac{d\phi(\vec{B})}{dt}=-\frac{1}{R}\frac{d}{dt}\int_{S}B_0\sqrt{1-\frac{2Rmg}{hL^2B_0^2}t}dt$$This is incorrect for two reasons: (a) the function $i(t)$ is not equal to its integral over time $t$ and (b) the integral is over time not over some surface $S$.

Write the correct integral expression formally, with the correct variable on the left hand side and maybe you will see what to do next and finish part (c).