- #1
brotherbobby
- 618
- 152
- Homework Statement
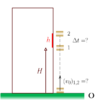
- Bond and Scaramanga get into a helicopter which begins to accelerate upward at ##a\;\text{m/s}^2## for ##3\;\text{s}## at which point Scaramanga gets thrown out. He bites the dust ##4.92\;\text{s}## after liftoff. (i) What was ##a##? (ii) From what height did Scaramanga get ejected?
- Relevant Equations
- The kinematic equations for uniform acceleration ##a_0## where all terms have their usual meanings. Just note that ##x(t_0)=x_0## and that ##v(t_0)=v_0##. We can choose ##t_0=0## here.
\begin{align}
&v(t)=v_0+a_0(t-t_0)\\
&x=x_0+v_0(t-t_0)+\dfrac{1}{2}a_0(t-t_0)^2\\
&v^2(x)=v^2_0+2a_0(x-x_0)\\
\end{align}
Substituting in ##(4)##,
\begin{align*}
-\frac{1}{2}at_1^2 &= at_1t_2-\frac{1}{2}gt_2^2\\
\Rightarrow \frac{1}{2}gt_2^2 &= at_1t_2+\frac{1}{2}at_1^2\\
\Rightarrow a(t_1t_2+\frac{1}{2}t_1^2) &=\frac{1}{2}gt_2^2\\
\Rightarrow at_1(2t_2+t_1)&=gt_2^2\\
\Rightarrow a &= \dfrac{gt_2^2}{t_1(2t_2+t_1)}\\
\Rightarrow a &= \dfrac{10\times 1.92^2}{3(2\times 1.92+3)}\\
\Rightarrow &\boxed{a=2.54\;\text{m/s}^2}
\end{align*}
The height at which the throwing off took place : ##h = \frac{1}{2}at_1^2=\frac{1}{2}\times 2.54\times 3^2=\boxed{11.43\;\text{m}}##
Request : I'd like to know where have I gone wrong. Was it in the meaning of the term "liftoff"?