How to compute the energy needed to compress the water isothermally?

[WMDhamnekar]

Hi,
Answer given is $E_n=29.4 Joules$ Here is the question.

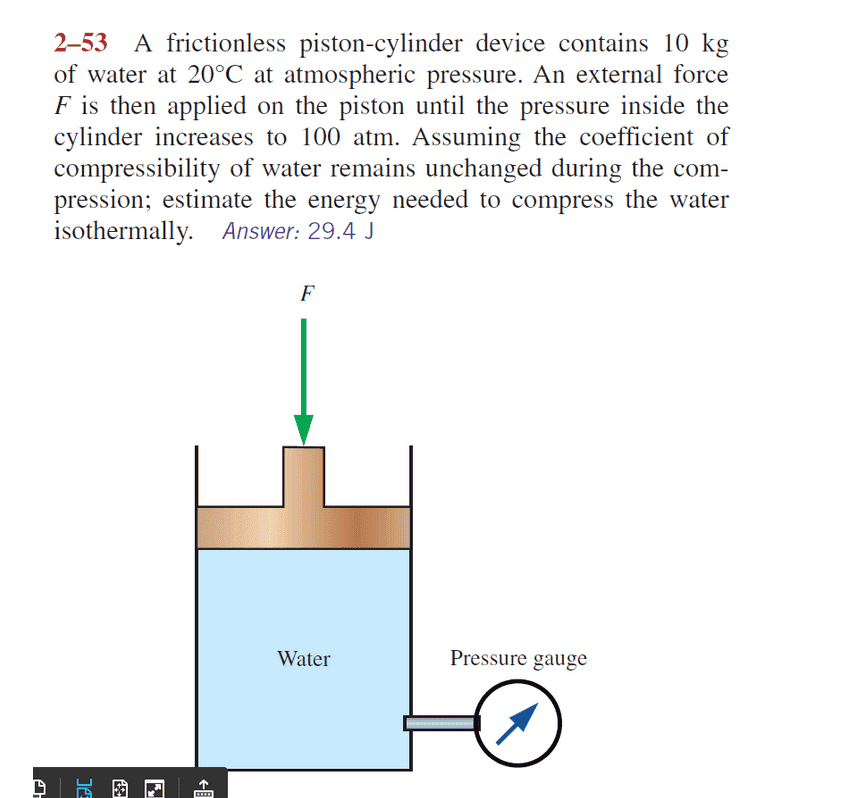
Answer provided by the Chemistry math expert/Professor is as follows but it is different from the answer given. How is that?

Compressibility is the fractional change in volume per unit increase in pressure. For each atmosphere increase in pressure, the volume of water would decrease 46.4 parts per million.
I'll pick a shape for the device, calculate distance traveled and force required, and use $work = force \times distance.$
with 100 atm, volume would decrease by 4640 PPM or by a factor of 0.00464

10 kg of water is about 10 liters or $0.01 m^3$

$100 atm = 1.013e7 Pa$ or $1.013e7 N/m^2$
assume a cube shape, height is $\sqrt[3]{0.01 m^3} = 0.2154435 m$ and base area is$ 0.0464159 m^2$ (coincidence that "464" appears as two different values)
force on piston is $1.013e7 N/m^2 \times 0.0464 m^2 = 470000 N$
that change in volume causes what change in height

new volume $= 0.01 m^3 – 0.01 m^3(0.00464) = 0.00995 m^3$

which has a height of $\frac{0.00995 m^3}{0.0464159 m^2} = 0.2143663 ,$

change is 0.2154435 – 0.2143663 = 0.00108 m
energy = Fd = (470000 N)(0.00108 m) = 506 JIs temperature of water $20^\circ C$ to be considered?

 

[I like Serena]

Answer given is $E_n=29.4 Joules$ Here is the question.

Answer provided by the Chemistry math expert/Professor is as follows but it is different from the answer given. How is that?
(snip)
force on piston is $1.013e7 N/m^2 \times 0.0464 m^2 = 470000 N$
that change in volume causes what change in height
new volume $= 0.01 m^3 – 0.01 m^3(0.00464) = 0.00995 m^3$
which has a height of $\frac{0.00995 m^3}{0.0464159 m^2} = 0.2143663 ,$
change is 0.2154435 – 0.2143663 = 0.00108 m

energy = Fd = (470000 N)(0.00108 m) = 506 J

Your expert's answer assumes that the force/pressure is constant at 100 atmosphere, but that is not the case.
Instead it will build up from 1 atmosphere up to 100 atmosphere.
So we can expect the actual answer to be about half of that $506\,J$, which is really an upper estimate.

I found $229\,J$ myself while taking the changing pressure into account with Calculus, which is indeed in the neighborhood of half of that $506\,J$.
Either way, it looks as if the answer of $29.4\,J$ is not correct.

Is temperature of water $20^\circ C$ to be considered?

We take the coefficient of isothermal compressibility of water at $20^\circ C$.
Wikipedia mentions that it is $4.4$ to $5.1×10^{-10}\, Pa^{-1}$ in ordinary conditions.
Close enough to that 46.4 parts per million that you mentioned.