- #1
Rectifier
Gold Member
- 313
- 4
This problem was translated from Swedish, sorry for any grammatical errors present.
The problem
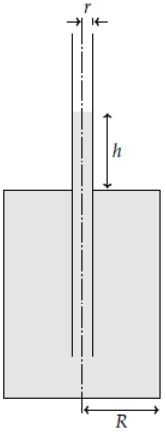
The grey is liquid is water. The small container is a pipe made of glas and the big container is a barrel. Water is poured into the glas pipe. When water reaches 12m over the barrel top(lid) the barrel breaks.
Calculate
a) the mass of the water in the glass pipe (over the lid)
b) the total force on the lid when the barrel breaks
Relevant equations
Liquid - water
h = 12m
R = 0.20m
r = 0.003m
(^^values from below the figure in my book)
##p=dgh##
The attempt
a)
Density is described by ## d = \frac{m}{V} ##
Volume of a cylinder is ##V = \pi r^2 h##
density for water is ##d = 1000 kg/m^3##
Mass is thus:
b)
There is a hole in the lid so I calculate the area of the doughnut.
The area of the lid is
I have only one more interesting formula in the book on this chapter - namely:
d = density
g = gravity at the surface of the material
h = height
I know that
d for water is = 1000 kg/m^3
g = 9.82
h = 12m
then
It feels like I should add atmospheric pressure somwhere but I am not 100% sure.
Please help :,(EDIT:
Apparently ## F_{total} = F_{water} + F_{air}##
and the foce from the air is
## F=p_{atm}A_L = 100kPa A_L = 100 \cdot 10^3 \pi (0.20 - 0.003)^2 = 12192.2...##
Thus ##F_{total} = F_{water} + F_{air} = 14367.3 N + 12192.2N =26559.5 N##
Does it look right?
The problem
The grey is liquid is water. The small container is a pipe made of glas and the big container is a barrel. Water is poured into the glas pipe. When water reaches 12m over the barrel top(lid) the barrel breaks.
Calculate
a) the mass of the water in the glass pipe (over the lid)
b) the total force on the lid when the barrel breaks
Relevant equations
Liquid - water
h = 12m
R = 0.20m
r = 0.003m
(^^values from below the figure in my book)
##p=dgh##
The attempt
a)
Density is described by ## d = \frac{m}{V} ##
Volume of a cylinder is ##V = \pi r^2 h##
density for water is ##d = 1000 kg/m^3##
Mass is thus:
## m = d \cdot V = d \cdot \pi r^2 h= 1000 kg/m^3 \cdot \pi (0.003)^2 12 = 0.339292... kg ##
b)
There is a hole in the lid so I calculate the area of the doughnut.
The area of the lid is
##A_L = \pi r_n^2 = \pi (R-r)^2 = \pi (0.20 - 0.003)^2 ##
The pressure is
##p = \frac{F}{A_L} \\ F=pA_L = \pi (0.20 - 0.003)^2p ##
I have only one more interesting formula in the book on this chapter - namely:
## p=dgh ##
where
d = density
g = gravity at the surface of the material
h = height
I know that
d for water is = 1000 kg/m^3
g = 9.82
h = 12m
then
##F=pA = A_Ldgh = 1000 \cdot 9.82 \cdot 12 \cdot \pi (0.20 - 0.003)^2 = 14367.3 N ##
It feels like I should add atmospheric pressure somwhere but I am not 100% sure.
Please help :,(EDIT:
Apparently ## F_{total} = F_{water} + F_{air}##
and the foce from the air is
## F=p_{atm}A_L = 100kPa A_L = 100 \cdot 10^3 \pi (0.20 - 0.003)^2 = 12192.2...##
Thus ##F_{total} = F_{water} + F_{air} = 14367.3 N + 12192.2N =26559.5 N##
Does it look right?
Last edited: