- #1
Memorical
- 4
- 2
- Homework Statement
- Find the minimum time it takes for a an object to start and end at rest for a given fixed acceleration, fixed deceleration and distance. Assume there is no maximum speed.
This can be modelled as a train travelling a given distance by accelerating until it hits the point where it needs to decelerate again. There is never a point of constant speed.
- Relevant Equations
- Kinematic equations:
d = 0.5 * a * t^2
Note: Maths has always been kinda a weak point for me in school. Anyway.
From hereon I'm going to talk about this in the context of a train for simplicity, even though this is actually needed for an entirely different context - but I don't think this is relevant for the problem.
In terms of my own individual working, I've attempted to break down the problem into two different sections:
Anyway, my current equations are as follows:
Now I start breaking things down into the acceleration/deceleration sections:
And this is where I'm stumped with trying to get D in terms of (ta+td) which would then give me an equation for T.
So I've gone to my friend for help, who's told me about using integration. I'll just paste screenshots of what was given to me for this:

as a representation of the problem to then plug into Wolfram Mathematica to solve for t:
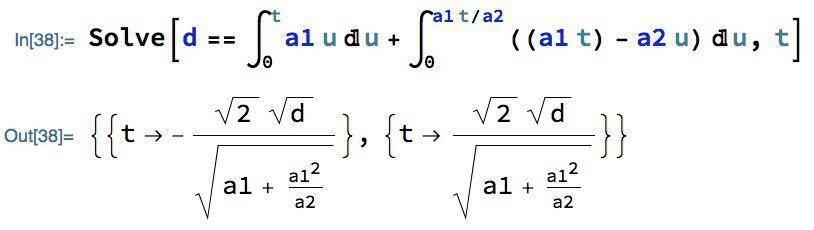
So of course we're never going to have negative time, so the positive answer has been used in my equations, however this is very much a black-box solution for me and therefore not really something I can work with and check it's correct, which is definitely an issue right now because I'm getting odd answers for T when putting in values of acceleration and deceleration. For instance, when I put in a higher value for deceleration, t goes up. Also I think if I swap acceleration and deceleration, t should remain the same, but they currently don't?
Can someone either verify for me that what's been given to me is definitely correct, or propose a different way for me to solve this, or just generally help/sanity check this for me?
Many thanks, and apologies for the wordy post! Edit: I also think I've put this under the wrong forum, but I'm unsure. Feel free to move this if that would be better!
From hereon I'm going to talk about this in the context of a train for simplicity, even though this is actually needed for an entirely different context - but I don't think this is relevant for the problem.
In terms of my own individual working, I've attempted to break down the problem into two different sections:
- Where the train accelerates to its maximum velocity,
- Then when it decelerates from this maximum velocity to rest.
Anyway, my current equations are as follows:
distance = 0.5 * velocity * time (based off from the area of a triangle)
acceleration = velocity / time (well known equation)
therefore: distance = 0.5 * acceleration * time^2 (also well known equation but figured I'd create it myself for the sanity checking)
Now I start breaking things down into the acceleration/deceleration sections:
Total Time (T) = ta + td
Total Distance (D) = da + dd
da = 0.5 * a * ta^2
dd = 0.5 * d * td^2
therefore: D = 0.5 * ((a * ta^2) + (d * td^2))
And this is where I'm stumped with trying to get D in terms of (ta+td) which would then give me an equation for T.
So I've gone to my friend for help, who's told me about using integration. I'll just paste screenshots of what was given to me for this:
as a representation of the problem to then plug into Wolfram Mathematica to solve for t:
So of course we're never going to have negative time, so the positive answer has been used in my equations, however this is very much a black-box solution for me and therefore not really something I can work with and check it's correct, which is definitely an issue right now because I'm getting odd answers for T when putting in values of acceleration and deceleration. For instance, when I put in a higher value for deceleration, t goes up. Also I think if I swap acceleration and deceleration, t should remain the same, but they currently don't?
Can someone either verify for me that what's been given to me is definitely correct, or propose a different way for me to solve this, or just generally help/sanity check this for me?
Many thanks, and apologies for the wordy post! Edit: I also think I've put this under the wrong forum, but I'm unsure. Feel free to move this if that would be better!
Last edited: