- #1
kshitij
- 218
- 27
- Homework Statement
- Consider two shapes of goal posts, one with a circular cross-section and the other with square. Which of these posts have a greater probability of a shot hitting the post, go in?
- Relevant Equations
- Laws of reflection
disclaimer: this is a made up question, so I don't know if there's a valid solution possible here
First let's talk about the square post,
it is clear that the shot will go in only if the ball hits the side AB of the square shown below, so the probability of a shot going in is simply ##\frac 1 3## as sides AB, BC & CD are equivalent and only hitting one of these 3 sides leads to a goal.

Now the interesting case of circular goal post,
In the figure below (top view of the goal post), any shot hitting the sector ADC will never go in, any shot hitting sector AB will always go in and any shot hitting sector BC will go in only when the angle of incidence is greater than the critical value. The critical value of angle of incidence happens when the reflected ray from the sector BC of one post hits the sector AB of the other post.

Limiting/critical incidence,

So now all we have to do is find the range of all the values of angle of incidence ##\theta## in sector BC for which the shot goes in i.e., [##\theta_{critial}##,##\frac \pi 2##] and then divide that by range of all permit-able values of ##\theta## i.e., [0,##\frac \pi 2##]
The problem is that this range of possible values of ##\theta## changes at every point on sector BC. And even though the length between posts and the radius of the posts are fixed, the value of ##\phi## (shown below) changes from [0,##\frac \pi 2##]
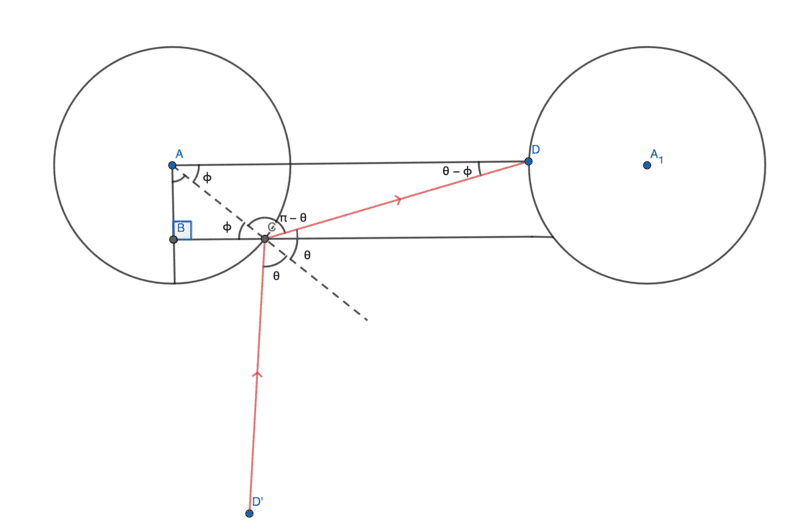
Now we can get a relation between ##\phi## & ##\theta## using sine law in ∆ADC,
$$ {\frac {\sin(\theta-\phi)} {AC}}={\frac {\sin(\pi-\theta)} {AD}}$$
here AC & AD are known (radius & distances between the posts respectively) and are constant but ##\theta## & ##\phi## are both variables
So that is my question, I want to find the critical value of ##\theta## for every value of ##\phi \in [0, \frac \pi 2]## i.e., first I want to individually calculate the probability of a shot going in for a particular value of ##\phi## then I'll add all the probabilities for every value of ##\phi \in [0, \frac \pi 2]##
So somehow I need to find,
$$\sum_{\phi=0}^\frac \pi 2 (\frac \pi 2 - \theta_{critical})$$
but the value of ##\theta## is non-linear and I don't know how to find that summation.
I don't know if this is the right way to do this or if there is any way of doing this?
In the end all I wanted was to find which shape of goal post is better? Square or circular, for most of the shots hitting the post, leading to a goal.
Any help is appreciated :)
Edit: to add a few assumptions I made in this post, the ball is a point mass moving with uniform speed in horizontal plane i.e., there is no vertical component of velocity of the ball, the ball is equally likely to come from any angle, there is no affect of spin on the ball, there is no friction at the point of collision.
The intent of this post was to find out that under similar conditions (i.e., under the assumptions I made) if we compare the square post with the circular one, which post is more likely to give us more goals after striking the post, that's it. I'm not interested in all possible ways of scoring goal via hitting the post, I just want the comparison that which of the two types of posts are better i.e., which of the two will offer us more goals!
First let's talk about the square post,
it is clear that the shot will go in only if the ball hits the side AB of the square shown below, so the probability of a shot going in is simply ##\frac 1 3## as sides AB, BC & CD are equivalent and only hitting one of these 3 sides leads to a goal.
Now the interesting case of circular goal post,
In the figure below (top view of the goal post), any shot hitting the sector ADC will never go in, any shot hitting sector AB will always go in and any shot hitting sector BC will go in only when the angle of incidence is greater than the critical value. The critical value of angle of incidence happens when the reflected ray from the sector BC of one post hits the sector AB of the other post.
Limiting/critical incidence,
So now all we have to do is find the range of all the values of angle of incidence ##\theta## in sector BC for which the shot goes in i.e., [##\theta_{critial}##,##\frac \pi 2##] and then divide that by range of all permit-able values of ##\theta## i.e., [0,##\frac \pi 2##]
The problem is that this range of possible values of ##\theta## changes at every point on sector BC. And even though the length between posts and the radius of the posts are fixed, the value of ##\phi## (shown below) changes from [0,##\frac \pi 2##]
Now we can get a relation between ##\phi## & ##\theta## using sine law in ∆ADC,
$$ {\frac {\sin(\theta-\phi)} {AC}}={\frac {\sin(\pi-\theta)} {AD}}$$
here AC & AD are known (radius & distances between the posts respectively) and are constant but ##\theta## & ##\phi## are both variables
So that is my question, I want to find the critical value of ##\theta## for every value of ##\phi \in [0, \frac \pi 2]## i.e., first I want to individually calculate the probability of a shot going in for a particular value of ##\phi## then I'll add all the probabilities for every value of ##\phi \in [0, \frac \pi 2]##
So somehow I need to find,
$$\sum_{\phi=0}^\frac \pi 2 (\frac \pi 2 - \theta_{critical})$$
but the value of ##\theta## is non-linear and I don't know how to find that summation.
I don't know if this is the right way to do this or if there is any way of doing this?
In the end all I wanted was to find which shape of goal post is better? Square or circular, for most of the shots hitting the post, leading to a goal.
Any help is appreciated :)
Edit: to add a few assumptions I made in this post, the ball is a point mass moving with uniform speed in horizontal plane i.e., there is no vertical component of velocity of the ball, the ball is equally likely to come from any angle, there is no affect of spin on the ball, there is no friction at the point of collision.
The intent of this post was to find out that under similar conditions (i.e., under the assumptions I made) if we compare the square post with the circular one, which post is more likely to give us more goals after striking the post, that's it. I'm not interested in all possible ways of scoring goal via hitting the post, I just want the comparison that which of the two types of posts are better i.e., which of the two will offer us more goals!
Last edited: