Fara_k2
- 1
- 0
Homework Statement
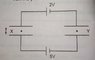
Two batteries are connected to two identical capacitors X and Y.Initially all the plates of the capacitors are uncharged.How to find charge on each Capacitor in the given diagram.Let the Capacitance of Capacitor be C.
Homework Equations
1.Q=CV
2.Kirchoff's law
3.C=C1+C2 ( Equivalent Capacitance for capacitors in parallel connection)
4.E=E1+E2(Equivalent emf for cells in series)
The Attempt at a Solution
I thought that there will be no charge on Y Capacitor as it is connected to negative terminal from both sides of 0 potential.
Q(on X)=CV( across X i.e.=3V)
Therefore Q=3C. But this answer is wrong. What is wrong in my approach?