zenterix
- 774
- 84
Thread moved from the technical forums to the schoolwork forums
TL;DR Summary: I am following the course 6.002 "Circuit and Electronics" on MIT OCW. There are no solutions to the problem sets. I would like to check my solution to one particular problem.
We are asked to find the equivalent resistance of the network
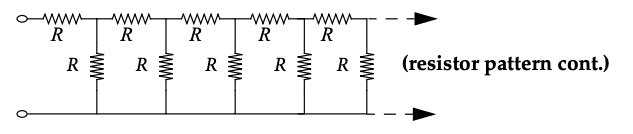
as viewed from its ports.
I simplified the network as
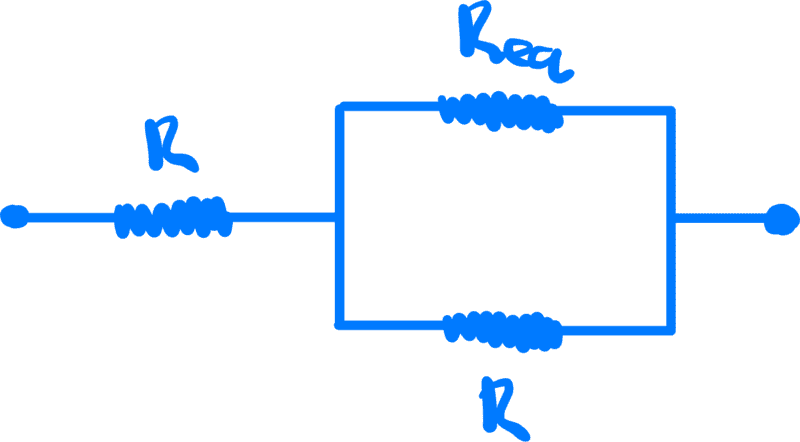
Where ##R_{eq}## is not only the equivalent resistance of the branch shown above, it is also the equivalent resistance of the entire network shown above (because the network shown above repeats itself infinitely).
Then
$$R_{eq}=R+\frac{R_{eq}R}{R+R_{eq}}$$
$$R_{eq}(R+R_{eq})=R(R+R_{eq})+RR_{eq}$$
$$R_{eq}^2=R^2+RR_{eq}$$
$$R_{eq}^2-RR_{eq}-R^2=0$$
$$\Delta = R^2+4R^2=5R^2$$
$$R_{eq}=\frac{R\pm R\sqrt{5}}{2}$$
$$=R\frac{1\pm\sqrt{5}}{2}$$
Is this result correct?
Here is the problem set in full if it is useful.
We are asked to find the equivalent resistance of the network
as viewed from its ports.
I simplified the network as
Where ##R_{eq}## is not only the equivalent resistance of the branch shown above, it is also the equivalent resistance of the entire network shown above (because the network shown above repeats itself infinitely).
Then
$$R_{eq}=R+\frac{R_{eq}R}{R+R_{eq}}$$
$$R_{eq}(R+R_{eq})=R(R+R_{eq})+RR_{eq}$$
$$R_{eq}^2=R^2+RR_{eq}$$
$$R_{eq}^2-RR_{eq}-R^2=0$$
$$\Delta = R^2+4R^2=5R^2$$
$$R_{eq}=\frac{R\pm R\sqrt{5}}{2}$$
$$=R\frac{1\pm\sqrt{5}}{2}$$
Is this result correct?
Here is the problem set in full if it is useful.
