gnits
- 137
- 46
- Homework Statement
- How to find the forces in a particular framework of light rods
- Relevant Equations
- Equating of forces
Could I please ask for help in how to do this question.
Is it in fact well formed, can it be solved as it is or do I need more information?
Q. Find the external forces and the force in each rod in the following framework of light rods which is supported and A and C:
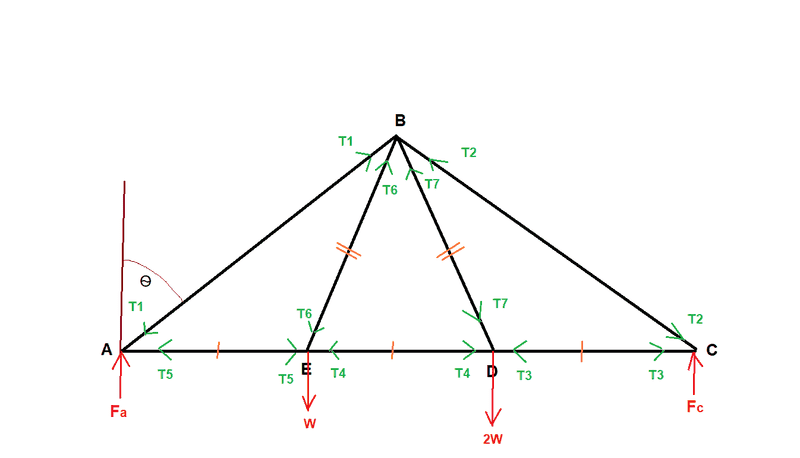
So, I need to find Fa, Fb and T1, T2, T3, T4, T5, T6 and T7 in terms of W.
I mark all forces as pointing towards the ends of the rods so that in the answers a negative value indicates a force towards the centre of a rod.
I call the length of the sides marked with a single bar "L".
I have labelled the angle Ѳ on the diagram for use in the following.
Taking the framework as a whole and resolving vertically gives:
Fa + Fc = 3W
Taking moments about A gives:
Fc * 3L = W * L + 2W * 2L and so this gives Fc = 5W/3 and so we also now know that Fa = 4W/3. These answers agree with the book answers.
Now, looking at the forces incident at A and resolving vertically we have:
T1 * cos(Ѳ) = 4W/3
and resolving horizontally we have that
T1 * sin(Ѳ) + T5 = 0.
From this, using cos^Ѳ + sin^Ѳ = 1 we can obtain:
16W^2 + 9*T5^2 = 9 * T1^2.
Now this agrees with the book answers for T5 and T1 (which are given individually), but I cannot see how to get them individually.
(In previous questions of this type I had always been provided with the angle of the figure - in this case, if I knew Ѳ then I could obtain T1 and T5 individually).
If I take the book answers for T1 and T5 and use my equations above I get that the principal value of Ѳ = 60 degrees. Does that need to be marked in the diagram for the question to be possible? Or should I be able to see how to derive the angle from the given geometry?
Here are the book answers:
T1 = 8W/3
T2 = 10W/3
T3 = -5*sqrt(3)W / 3
T4 = -sqrt(3)W
T5 = -4*sqrt(3)W/3
T6 = -4*sqrt(3)W/3
T7 = -2*sqrt(3)W/3
Thanks for any help.
Is it in fact well formed, can it be solved as it is or do I need more information?
Q. Find the external forces and the force in each rod in the following framework of light rods which is supported and A and C:
So, I need to find Fa, Fb and T1, T2, T3, T4, T5, T6 and T7 in terms of W.
I mark all forces as pointing towards the ends of the rods so that in the answers a negative value indicates a force towards the centre of a rod.
I call the length of the sides marked with a single bar "L".
I have labelled the angle Ѳ on the diagram for use in the following.
Taking the framework as a whole and resolving vertically gives:
Fa + Fc = 3W
Taking moments about A gives:
Fc * 3L = W * L + 2W * 2L and so this gives Fc = 5W/3 and so we also now know that Fa = 4W/3. These answers agree with the book answers.
Now, looking at the forces incident at A and resolving vertically we have:
T1 * cos(Ѳ) = 4W/3
and resolving horizontally we have that
T1 * sin(Ѳ) + T5 = 0.
From this, using cos^Ѳ + sin^Ѳ = 1 we can obtain:
16W^2 + 9*T5^2 = 9 * T1^2.
Now this agrees with the book answers for T5 and T1 (which are given individually), but I cannot see how to get them individually.
(In previous questions of this type I had always been provided with the angle of the figure - in this case, if I knew Ѳ then I could obtain T1 and T5 individually).
If I take the book answers for T1 and T5 and use my equations above I get that the principal value of Ѳ = 60 degrees. Does that need to be marked in the diagram for the question to be possible? Or should I be able to see how to derive the angle from the given geometry?
Here are the book answers:
T1 = 8W/3
T2 = 10W/3
T3 = -5*sqrt(3)W / 3
T4 = -sqrt(3)W
T5 = -4*sqrt(3)W/3
T6 = -4*sqrt(3)W/3
T7 = -2*sqrt(3)W/3
Thanks for any help.
Last edited: