How to find the velocity of a wave in simple harmonic motion given time

[MattDutra123]

Homework Statement

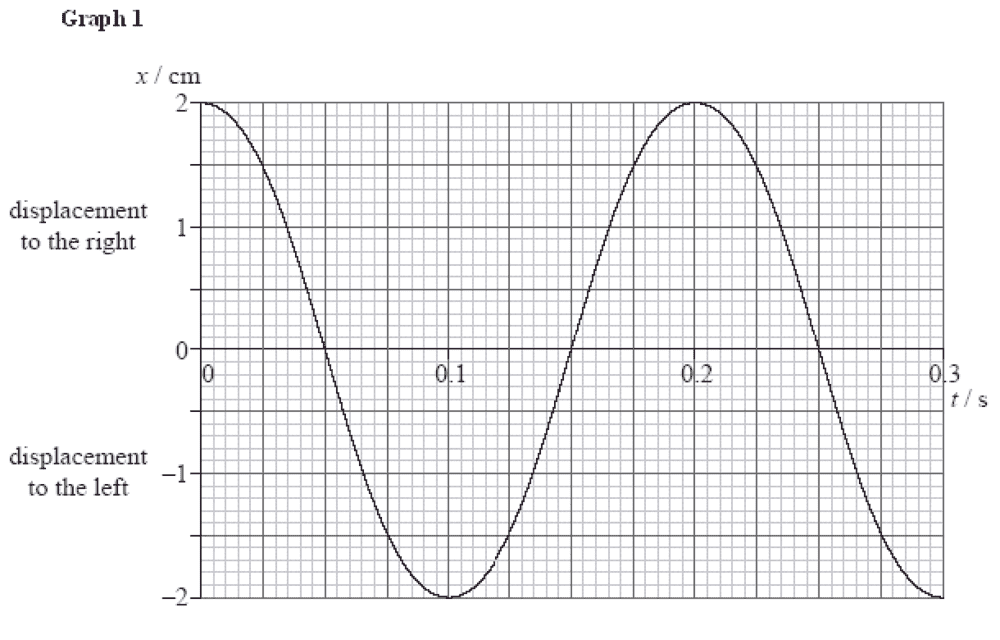
Find the speed of this longitudinal wave at t=0.12s.

Relevant Equations

v=w*xmax*cos(wt)

The graph provided is below. The problem asks for the speed of the wave at 0.12s. I used the formula v=w*xmax*cos(wt), provided in our textbook where xmax is the amplitude of 2 cm, w (omega) is 2pi divided by the period of 0.2. However, for some reason this formula doesn't give me the correct result. Instead, the solution to the problem involves the formula w*sqrt(xmax^2-x^2), which requires us to first find the displacement at t = 0.12.

My question is: why does the formula I used not work? Why must we use the other formula to solve this problem? I apologise for the bad formatting of the formulas.

 

[kuruman]

It doesn't work because it's the wrong formula to use. It predicts that the velocity is maximum at t = 0. If you look at the graph, the position is maximum at t = 0 which means that the speed is zero at t = 0.

Also, is this a wave or a simple harmonic oscillator? I think the latter.

 

[MattDutra123]

It doesn't work because it's the wrong formula. It predicts that the velocity is maximum at t = 0. If you look at the graph, the position is maximum at t = 0 which means that the speed is zero at t = 0.

Also, is this a wave or a simple harmonic oscillator? I think the latter.

Why does the formula I used predict that velocity is maximum at t=0?
If I use the same formula but replacing cos with sin, I get the correct answer. Why is that? Is it related to what you said? We were taught to use cos when displacement is maximum at t = 0, and sine when displacement is 0 at t = 0. Is this correct?

 

[kuruman]

You wrote
$v(t)=\omega~ x_{max}\cos(\omega~t)$
At $t = 0$, $v(0)=\omega~ x_{max}\cos(0)=\omega~ x_{max}(1)\neq 0.$
Try this
1. Find an expression for $x(t)$ consistent with the graph. Hint: As indicated above, $x_{max}\cos(0)=x_{max}.$
2. Take the derivative with respect to time to find $v(t)$. The result should answer your second question.
3. Evaluate $v(t=0.12~s).$ This method is neater and there is no need to do what the solution suggests.

We were taught to use cos when displacement is maximum at t = 0, and sine when displacement is 0 at t = 0. Is this correct?

That is correct. Your mistake was that you used cos for the velocity; you were taught to use cos for the displacement.