How to find the voltage threshold at which diode switches states?

Join the discussion
Registration is free. Ask a follow-up in this thread, or start your own.
Sign up Log in
4 replies · 2K views
Andrei0408
Messages
50
Reaction score
8
Homework Statement
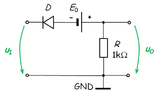
The diode in the figure is described by its offset model: U_D0=0.6V and r_d=0. Knowing that E_0=3.9V, find the voltage threshold u_l, at which the diode switches to its opposite state.
Relevant Equations
u_l=−u_D−i_D * R
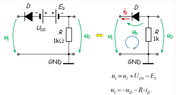
I've attached pictures with the circuit and part of the attempted solution. I've replaced the diode with its offset model and obtained the equivalent circuit in the 2nd picture. After applying KVL, I've obtained that u_l=−u_D−i_D*R. Since U_D0 is greater than 0, I've deduced that the diode must be ON in this case, therefore u_D=0, so u_l=−i_D*R. The problem is I don't know how to find i_D so I can calculate u_l. The answer for this problem should be, according to the book, −4.5 . Any ideas? Thank you!
 
Attachments
  • Screenshot_13.png
    Screenshot_13.png
    7.5 KB · Views: 201
  • received_461045691428275.png
    received_461045691428275.png
    11.8 KB · Views: 202
Physics news on Phys.org

Discussion

What is the diode current right at the threshold of switching? How does that effect your KVL equation?

So, let's say you started with a very negative input voltage, so you know the diode is conducting, what happens as you increase that input towards the switching threshold?
 
Well, when the diode switches to its OFF state, the current should be 0, U_D should be negative, so we could replace the diode with an open circuit, since there is no current
 
Andrei0408 said:
Well, when the diode switches to its OFF state, the current should be 0, U_D should be negative, so we could replace the diode with an open circuit, since there is no current
Yes, so how can you use that fact in the equations you created? What is KVL right at the threshold, when the current first reaches 0? What is the largest input voltage you can have and still have forward diode current (let's say 1uA)?
 
DaveE said:
Yes, so how can you use that fact in the equations you created? What is KVL right at the threshold, when the current first reaches 0? What is the largest input voltage you can have and still have forward diode current (let's say 1uA)?
Since the answer we're looking for should be -4.5V, I've observed that this could be -(0.6+3.9). So using this logic, u_D = E_0 and i_D * R = U_D0. Is this correct?
EDIT: I think I may have understood: if the diode is OFF then the input voltage is negative, which is why u_l = -U_D0 - E_0, please correct me if I'm wrong
 
Last edited: