I How to get plot (optical gain of GaAs)?

[yeyintkoko]

How can i calculate this plot (photon energy dependence of the optical gain (or loss = negative gain) of GaAs with the injected carrier density as a parameter?
Show calculated plot based on this equation

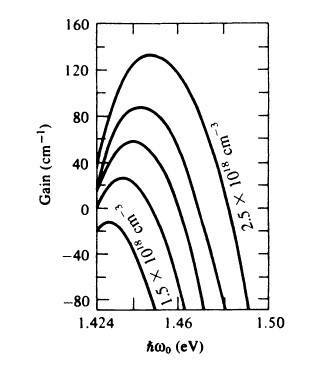
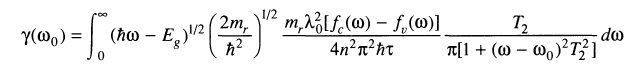
Given parameter:
m_c=0.067 m_e; (effective mass of electrons in conduction band)
m_v=0.48 m_e; (effective mass of holes in valence band)
T₂~0.5 ps; (lifetime for coherent interaction of electrons with a monochromatic field)
E_g=1.43 eV; (energy band gap of GaAs)
taung~3x10^-9s; (recombination lifetime)
1/m_r=1/m_c+1/m_v; ( reduced effective mass)
n= 3.6: (refractive index for GaAs)

How can i find this value
ħω (energy of photon)- this should be ħω>E_g. How can i determine this energy?
λ₀
ω₀ ( if i known λ₀, can i get ω₀? (ω=c/λ))
[ƒ_c(ω)-ƒ_v(ω)]

Really I need your help. I am new for semiconductor laser. Please anyone help me.
Thanks!

 

[deep4g]

please suggest me the books, where from you got this equation ?????