Discussion Overview
The discussion revolves around measuring time in a reference frame using a light clock, particularly focusing on the implications of time dilation and the relationship between different reference frames. Participants explore the calculations and concepts related to the time measured by a clock in motion versus a clock at rest, as well as the distances involved in these scenarios.
Discussion Character
- Exploratory
- Technical explanation
- Debate/contested
- Mathematical reasoning
Main Points Raised
- Some participants propose that the time measured in a moving reference frame is Δt0, but express uncertainty about this assumption.
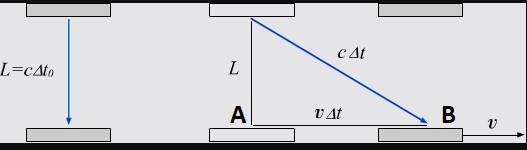
- Others argue that the distance covered by light in a moving clock is not cΔt0 but cΔt, suggesting a need for clarity in the definitions of time and distance in different frames.
- One participant emphasizes the importance of computing the position of the light pulse at different points in time to understand the time taken for the light to travel between points A and B.
- There is confusion regarding the representation of the diagrams, with participants questioning the accuracy of the illustrations and their implications for the discussion.
- Some participants clarify that the clock in the moving frame is at rest, leading to further questions about the time measured by that clock during motion.
- One participant attempts to rephrase the question and seeks to establish an equation for the moving reference frame, indicating a desire for mathematical clarity.
Areas of Agreement / Disagreement
Participants do not reach a consensus on the correct interpretation of time measurement in moving versus stationary frames. Multiple competing views and interpretations remain throughout the discussion.
Contextual Notes
There are limitations in the discussion regarding the assumptions made about the definitions of time and distance in different reference frames, as well as the mathematical relationships involved. Some participants express confusion over the application of Pythagorean theorem to the scenarios presented.
Who May Find This Useful
This discussion may be useful for individuals interested in the concepts of time dilation, reference frames in relativity, and the mathematical relationships governing light clocks in different states of motion.