cwill53
- 220
- 40
- Homework Statement
- Evaluate the following integral in cylindrical coordinates.
$$\int_0^6 \int_0^{\frac{\sqrt{2}}{2}}\int_x^{\sqrt{1-x^2}}e^{-x^2-y^2} \, dy \, dx \, dz$$
After attempting to set the bounds in cylindrical coordinates, I got
$$\int_0^6 \int_0^{\frac{\sqrt{2}}{2}}\int_{\rho \cos\varphi }^{\sqrt{1-\rho^2 \cos^2\varphi }}e^{-\rho ^2}d\varphi \rho \, d\rho \, dz$$
But I know this doesn't make sense. Can someone explain how to switch the bounds analytically? I don't understand how to transform the bounds.
I had posted this question on the Mathematics Stack Exchange:
https://math.stackexchange.com/questions/3898044/how-to-set-bounds-in-cylindrical-coordinates
- Relevant Equations
- $$\begin{cases}x=\rho \cos \phi \\
y= \rho \sin \phi \\
z=z'\end{cases}$$
I'm trying to evaluate the following integral in cylindrical coordinates.
$$\int_0^6 \int_0^{\frac{\sqrt{2}}{2}}\int_x^{\sqrt{1-x^2}}e^{-x^2-y^2} \, dy \, dx \, dz$$
After attempting to set the bounds in cylindrical coordinates, I got
$$\int_0^6 \int_0^{\frac{\sqrt{2}}{2}}\int_{\rho \cos\varphi }^{\sqrt{1-\rho^2 \cos^2\varphi }}e^{-\rho ^2}d\varphi \rho \, d\rho \, dz$$
But I know this doesn't make sense. Can someone explain how to switch the bounds analytically? I don't understand how to transform the bounds.
I had posted this question on the Mathematics Stack Exchange:
https://math.stackexchange.com/questions/3898044/how-to-set-bounds-in-cylindrical-coordinates
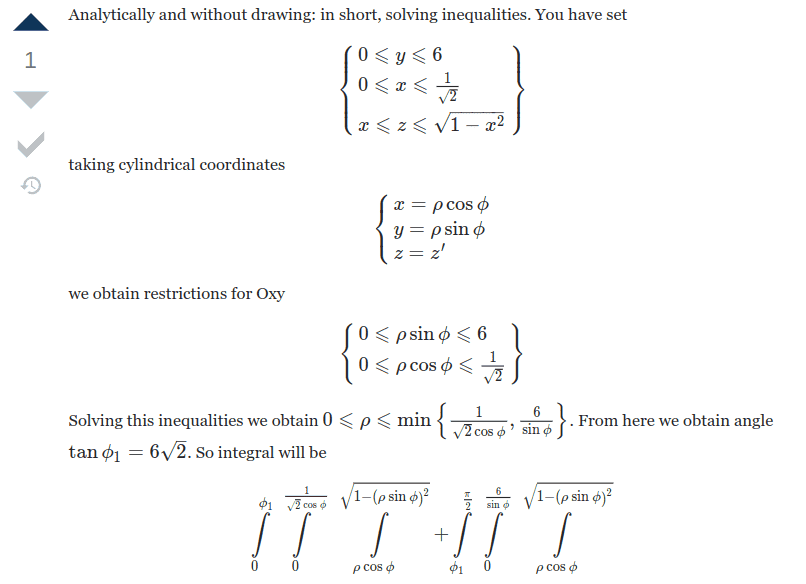
This is what one poster said. But the z-coordinate, not the y-coordinate, is what varies from 0 to 6.
So the inequality should be
However I need some assistance solving the inequality so that it would help me set the bounds.
$$\int_0^6 \int_0^{\frac{\sqrt{2}}{2}}\int_x^{\sqrt{1-x^2}}e^{-x^2-y^2} \, dy \, dx \, dz$$
After attempting to set the bounds in cylindrical coordinates, I got
$$\int_0^6 \int_0^{\frac{\sqrt{2}}{2}}\int_{\rho \cos\varphi }^{\sqrt{1-\rho^2 \cos^2\varphi }}e^{-\rho ^2}d\varphi \rho \, d\rho \, dz$$
But I know this doesn't make sense. Can someone explain how to switch the bounds analytically? I don't understand how to transform the bounds.
I had posted this question on the Mathematics Stack Exchange:
https://math.stackexchange.com/questions/3898044/how-to-set-bounds-in-cylindrical-coordinates
This is what one poster said. But the z-coordinate, not the y-coordinate, is what varies from 0 to 6.
So the inequality should be
| $$\left\lbrace \begin{array}{a} x\leqslant \rho \sin \phi \leqslant \sqrt{1-x^{2}}\\ 0 \leqslant \rho \cos \phi \leqslant \frac{1}{\sqrt{2}} \end{array} \right\rbrace$$ |