physicshawk
- 11
- 0
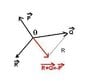
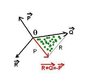
A particle is in equilibrium under the action of three horizontal forces P, Q and R. The magnitudes of P, Q and R are 25 N, Q N, and R N respectively, and the cosine of the angle between P and Q is -0.96.
Show that R^2 = (Q - 24)^2 + 7^2.
Hence find:
(a) the least possible value of R,
(b) the corresponding angle between Q and R.
My working:
R^2 = P^2 + Q^2 - 2(P)(Q) Cos (theta)
R^2 = 25^2 + Q^2 - 2(25) (Q) (-0.96)
R^2= 25^2 + Q^2 + 48 Q
R^2 = Q^2 + 48Q + 25^2
Now, I was trying completing the squares but... i don't know how to proceed. Please Help.
Show that R^2 = (Q - 24)^2 + 7^2.
Hence find:
(a) the least possible value of R,
(b) the corresponding angle between Q and R.
My working:
R^2 = P^2 + Q^2 - 2(P)(Q) Cos (theta)
R^2 = 25^2 + Q^2 - 2(25) (Q) (-0.96)
R^2= 25^2 + Q^2 + 48 Q
R^2 = Q^2 + 48Q + 25^2
Now, I was trying completing the squares but... i don't know how to proceed. Please Help.
Last edited: